Advertisements
Advertisements
Question
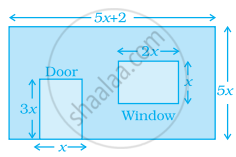
The figure shows the dimensions of a wall having a window and a door of a room. Write an algebraic expression for the area of the wall to be painted.
Solution
We have a wall of dimension 5x × (5x + 2) having a window and a door of dimension (2x × x) and (3x × x), respectively.
Then, area of the window = 2x × x = 2x2 sq.units
Area of the door = 3x × x = 3x2 sq.units
And area of wall = (5x + 2) × 5x = (25x2 + 10x) sq.units
Now, area of the required part of the wall to be painted
= Area of the wall – (Area of the window + Area of the door)
= 25x2 + 10x – (2x2 + 3x2)
= 25x2 + 10x – 5x2
= 20x2 + 10x
= 2 × 2 × 5 × x × x + 2 × 5 × x
= 2 × 5 × x(2x + 1)
= 10x(2x + 1) sq.units
APPEARS IN
RELATED QUESTIONS
Get the algebraic expression in the following case using variables, constants and arithmetic operation.
Subtraction of z from y
Factorize `[x^2 + 1/x^2] - 4[x + 1/x] + 6`
(x + y)3 − (x − y)3 can be factorized as
Separate the constants and variables from the following :
`-7,7+"x",7"x"+"yz",sqrt5,sqrt("xy"),(3"yz")/8,4.5"y"-3"x",`
8 −5, 8 − 5x, 8x −5y × p and 3y2z ÷ 4x
Divide: - 16ab2c by 6abc
The area of a rectangular field is 25x2 + 20xy + 3y2 square unit. If its length is 5x + 3y unit, find its breadth, Hence find its perimeter.
Complete the table.
| × | 2x2 | −2xy | x4y3 | 2xyz | (___)xz2 |
| x4 | |||||
| (___) | 4x5y4 | ||||
| −x2y | |||||
| 2y2z | −10xy2z3 | ||||
| −3xyz | |||||
| (___) | −14xyz2 |
The value of 3x2 – 5x + 3 when x = 1 is ______.
The rate of planting the grass is ₹ x per square metre. Find the cost of planting the grass on a triangular lawn whose base is y metres and height is z metres.
Express the following properties with variables x, y and z.
Associative property of addition
