Advertisements
Chapters
2: Data Handling
3: Square-Square Root and Cube-Cube Root
4: Linear Equation In One Variable
5: Understanding Quadrilaterals and Practical Geometry
6: Visualising Solid Shapes
▶ 7: Algebraic Expression, Identities and Factorisation
8: Exponents and Powers
9: Comparing Quantities
10: Direct and Inverse Proportions
11: Mensuration
12: Introduct To Graphs
13: Playing With Numbers
![NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 7 - Algebraic Expression, Identities and Factorisation NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 7 - Algebraic Expression, Identities and Factorisation - Shaalaa.com](/images/mathematics-english-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 7: Algebraic Expression, Identities and Factorisation
Below listed, you can find solutions for Chapter 7 of CBSE NCERT Exemplar for Mathematics [English] Class 8.
NCERT Exemplar solutions for Mathematics [English] Class 8 7 Algebraic Expression, Identities and Factorisation Exercise [Pages 224 - 240]
Choose the correct alternative:
The product of a monomial and a binomial is a ______.
Monomial
Binomial
Trinomial
None of these
In a polynomial, the exponents of the variables are always ______.
Integers
Positive integers
Non-negative integers
Non-positive integers
Which of the following is correct?
(a – b)2 = a2 + 2ab – b2
(a – b)2 = a2 – 2ab + b2
(a – b)2 = a2 – b2
(a + b)2 = a2 + 2ab – b2
The sum of –7pq and 2pq is ______.
–9pq
9pq
5pq
– 5pq
If we subtract –3x2y2 from x2y2, then we get ______.
– 4x2y2
– 2x2y2
2x2y2
4x2y2
Like term as 4m3n2 is ______.
4m2n2
– 6m3n2
6pm3n2
4m3n
Which of the following is a binomial?
7 × a + a
6a2 + 7b + 2c
4a × 3b × 2c
6(a2 + b)
Sum of a – b + ab, b + c – bc and c – a – ac is ______.
2c + ab – ac – bc
2c – ab – ac – bc
2c + ab + ac + bc
2c – ab + ac + bc
Product of the following monomials 4p, – 7q3, –7pq is ______.
196 p2q4
196 pq4
– 196 p2q4
196 p2q3
Area of a rectangle with length 4ab and breadth 6b2 is ______.
24a2b2
24ab3
24ab2
24ab
Volume of a rectangular box (cuboid) with length = 2ab, breadth = 3ac and height = 2ac is ______.
12a3bc2
12a3bc
12a2bc
2ab + 3ac + 2ac
Product of 6a2 – 7b + 5ab and 2ab is ______.
12a3b – 14ab2 + 10ab
12a3b – 14ab2 + 10a2b2
6a2 – 7b + 7ab
12a2b – 7ab2 + 10ab
Square of 3x – 4y is ______.
9x2 – 16y2
6x2 – 8y2
9x2 + 16y2 + 24xy
9x2 + 16y2 – 24xy
Which of the following are like terms?
5xyz2, – 3xy2z
– 5xyz2, 7xyz2
5xyz2, 5x2yz
5xyz2, x2y2z2
Coefficient of y in the term `(-y)/3` is ______.
– 1
– 3
`(-1)/3`
`1/3`
a2 – b2 is equal to ______.
(a – b)2
(a – b)(a – b)
(a + b)(a – b)
(a + b)(a + b)
Common factor of 17abc, 34ab2, 51a2b is ______.
17abc
17ab
17ac
17a2b2c
Square of 9x – 7xy is ______.
81x2 + 49x2y2
81x2 – 49x2y2
81x2 + 49x2y2 – 126x2y
81x2 + 49x2y2 – 63x2y
Factorised form of 23xy – 46x + 54y – 108 is ______.
(23x + 54)(y – 2)
(23x + 54y)(y – 2)
(23xy + 54y)(– 46x – 108)
(23x + 54)(y + 2)
Factorised form of r2 – 10r + 21 is ______.
(r – 1)(r – 4)
(r – 7)(r – 3)
(r – 7)(r + 3)
(r + 7)(r + 3)
Factorised form of p2 – 17p – 38 is ______.
(p – 19)(p + 2)
(p – 19)(p – 2)
(p + 19)(p + 2)
(p + 19)(p – 2)
On dividing 57p2qr by 114pq, we get ______.
`1/4 pr`
`3/4 pr`
`1/2 pr`
`2pr`
On dividing p(4p2 – 16) by 4p(p – 2), we get ______.
2p + 4
2p – 4
p + 2
p – 2
The common factor of 3ab and 2cd is ______.
1
– 1
a
c
An irreducible factor of 24x2y2 is ______.
x2
y2
x
24x
Number of factors of (a + b)2 is ______.
4
3
2
1
The factorised form of 3x – 24 is ______.
3x × 24
3(x – 8)
24(x – 3)
3(x – 12)
The factors of x2 – 4 are ______.
(x – 2),(x – 2)
(x + 2),(x – 2)
(x + 2),(x + 2)
(x – 4),(x – 4)
The value of (– 27x2y) ÷ (– 9xy) is ______.
3xy
– 3xy
– 3x
3x
The value of (2x2 + 4) ÷ 2 is ______.
2x2 + 2
x2 + 2
x2 + 4
2x2 + 4
The value of (3x3 + 9x2 + 27x) ÷ 3x is ______.
x2 + 9 + 27x
3x3 + 3x2 + 27x
3x3 + 9x2 + 9
x2 + 3x + 9
The value of (a + b)2 + (a – b)2 is ______.
2a + 2b
2a – 2b
2a2 + 2b2
2a2 – 2b2
The value of (a + b)2 – (a – b)2 is ______.
4ab
– 4ab
2a2 + 2b2
2a2 – 2b2
Fill in the blanks:
The product of two terms with like signs is a ______ term.
The product of two terms with unlike signs is a ______ term.
a(b + c) = a × ____ + a × _____.
(a – b) ______ = a2 – 2ab + b2
a2 – b2 = (a + b) ______.
(a – b)2 + ______ = a2 – b2
(a + b)2 – 2ab = ______ + ______.
(x + a)(x + b) = x2 + (a + b)x + ______.
The product of two polynomials is a ______.
Common factor of ax2 + bx is ______.
Factorised form of 18 mn + 10 mnp is ______.
Factorised form of 4y2 – 12y + 9 is ______.
38x3y2z ÷ 19xy2 is equal to ______.
Volume of a rectangular box with length 2x, breadth 3y and height 4z is ______.
672 – 372 = (67 – 37) × ______ = ______.
1032 – 1022 = ______ × (103 – 102) = ______.
Area of a rectangular plot with sides 4x2 and 3y2 is ______.
Volume of a rectangular box with l = b = h = 2x is ______.
The coefficient in – 37abc is ______.
Number of terms in the expression a2 + bc × d is ______.
The sum of areas of two squares with sides 4a and 4b is ______.
The common factor method of factorisation for a polynomial is based on ______ property.
The side of the square of area 9y2 is ______.
On simplification `(3x + 3)/3` = ______.
The factorisation of 2x + 4y is ______.
State whether the following statement is True or False:
(a + b)2 = a2 + b2
True
False
(a – b)2 = a2 – b2
True
False
(a + b)(a – b) = a2 – b2
True
False
The product of two negative terms is a negative term.
True
False
The product of one negative and one positive term is a negative term.
True
False
The coefficient of the term – 6x2y2 is – 6.
True
False
p2q + q2r + r2q is a binomial.
True
False
The factors of a2 – 2ab + b2 are (a + b) and (a + b).
True
False
h is a factor of 2π (h + r).
True
False
Some of the factors of `n^2/2 + n/2` are `1/2, n` and (n + 1).
True
False
An equation is true for all values of its variables.
True
False
x2 + (a + b)x + ab = (a + b)(x + ab)
True
False
Common factor of 11pq2, 121p2q3, 1331p2q is 11p2q2.
True
False
Common factor of 12a2b2 + 4ab2 – 32 is 4.
True
False
Factorisation of – 3a2 + 3ab + 3ac is 3a(– a – b – c).
True
False
Factorised form of p2 + 30p + 216 is (p + 18)(p – 12).
True
False
The difference of the squares of two consecutive numbers is their sum.
True
False
abc + bca + cab is a monomial.
True
False
On dividing `p/3` by `3/p`, the quotient is 9.
True
False
The value of p for 512 – 492 = 100p is 2.
True
False
(9x – 51) ÷ 9 is x – 51.
True
False
The value of (a + 1)(a – 1)(a2 + 1) is a4 – 1.
True
False
Add:
7a2bc, –3abc2, 3a2bc, 2abc2
Add:
9ax + 3by – cz, –5by + ax + 3cz
Add:
xy2z2 + 3x2y2z – 4x2yz2, – 9x2y2z + 3xy2z2 + x2yz2
Add:
5x2 – 3xy + 4y2 – 9, 7y2 + 5xy – 2x2 + 13
Add:
2p4 – 3p3 + p2 – 5p + 7, –3p4 – 7p3 – 3p2 – p – 12
Add:
3a(a – b + c), 2b(a – b + c)
Add:
3a(2b + 5c), 3c(2a + 2b)
Subtract:
5a2b2c2 from –7a2b2c2
Subtract:
6x2 – 4xy + 5y2 from 8y2 + 6xy – 3x2
Subtract:
2ab2c2 + 4a2b2c – 5a2bc2 from –10a2b2c + 4ab2c2 + 2a2bc2
Subtract:
3t4 – 4t3 + 2t2 – 6t + 6 from – 4t4 + 8t3 – 4t2 – 2t + 11
Subtract:
2ab + 5bc – 7ac from 5ab – 2bc – 2ac + 10abc
Subtract:
7p(3q + 7p) from 8p(2p – 7q)
Subtract:
–3p2 + 3pq + 3px from 3p(– p – a – r)
Multiply the following:
–7pq2r3, –13p3q2r
Multiply the following:
3x2y2z2, 17xyz
Multiply the following:
15xy2, 17yz2
Multiply the following:
–5a2bc, 11ab, 13abc2
Multiply the following:
–3x2y, (5y – xy)
Multiply the following:
abc, (bc + ca)
Multiply the following:
7pqr, (p – q + r)
Multiply the following:
x2y2z2, (xy – yz + zx)
Multiply the following:
(p + 6), (q – 7)
Multiply the following:
6mn, 0mn
Multiply the following:
a, a5, a6
Multiply the following:
–7st, –1, –13st2
Multiply the following:
b3, 3b2, 7ab5
Multiply the following:
`- 100/9 rs; 3/4 r^3s^2`
Multiply the following:
(a2 – b2), (a2 + b2)
Multiply the following:
(ab + c), (ab + c)
Multiply the following:
(pq – 2r), (pq – 2r)
Multiply the following:
`(3/4x - 4/3 y), (2/3x + 3/2y)`
Multiply the following:
`3/2 p^2 + 2/3 q^2, (2p^2 - 3q^2)`
Multiply the following:
(x2 – 5x + 6), (2x + 7)
Multiply the following:
(3x2 + 4x – 8), (2x2 – 4x + 3)
Multiply the following:
(2x – 2y – 3), (x + y + 5)
Simplify:
(3x + 2y)2 + (3x – 2y)2
Simplify:
(3x + 2y)2 – (3x – 2y)2
Simplify:
`(7/9 a + 9/7 b)^2 - ab`
Simplify:
`(3/4x - 4/3y)^2 + 2xy`
Simplify:
(1.5p + 1.2q)2 – (1.5p – 1.2q)2
Simplify:
(2.5m + 1.5q)2 + (2.5m – 1.5q)2
Simplify:
(x2 – 4) + (x2 + 4) + 16
Simplify:
(ab – c)2 + 2abc
Simplify:
(a – b) (a2 + b2 + ab) – (a + b) (a2 + b2 – ab)
Simplify:
(b2 – 49)(b + 7) + 343
Simplify:
(4.5a + 1.5b)2 + (4.5b + 1.5a)2
Simplify:
(pq – qr)2 + 4pq2r
Simplify:
(s2t + tq2)2 – (2stq)2
Expand the following, using suitable identities.
(xy + yz)2
Expand the following, using suitable identities.
(x2y – xy2)2
Expand the following, using suitable identities.
`(4/5a + 5/4b)^2`
Expand the following, using suitable identities.
`(2/3x - 3/2y)^2`
Expand the following, using suitable identities.
`(4/5p + 5/3q)^2`
Expand the following, using suitable identities.
(x + 3)(x + 7)
Expand the following, using suitable identities.
(2x + 9)(2x – 7)
Expand the following, using suitable identities.
`((4x)/5 + y/4)((4x)/5 + (3y)/4)`
Expand the following, using suitable identities.
`((2x)/3 - 2/3)((2x)/3 + (2a)/3)`
Expand the following, using suitable identities.
(2x – 5y)(2x – 5y)
Expand the following, using suitable identities.
`((2a)/3 + b/3)((2a)/3 - b/3)`
Expand the following, using suitable identities.
(x2 + y2)(x2 – y2)
Expand the following, using suitable identities.
(a2 + b2)2
Expand the following, using suitable identities.
(7x + 5)2
Expand the following, using suitable identities.
(0.9p – 0.5q)2
Expand the following, using suitable identities.
x2y2 = (xy)2
Using suitable identities, evaluate the following.
(52)2
Using suitable identities, evaluate the following.
(49)2
Using suitable identities, evaluate the following.
(103)2
Using suitable identities, evaluate the following.
(98)2
Using suitable identities, evaluate the following.
(1005)2
Using suitable identities, evaluate the following.
(995)2
Using suitable identities, evaluate the following.
47 × 53
Using suitable identities, evaluate the following.
52 × 53
Using suitable identities, evaluate the following.
105 × 95
Using suitable identities, evaluate the following.
104 × 97
Using suitable identities, evaluate the following.
101 × 103
Using suitable identities, evaluate the following.
98 × 103
Using suitable identities, evaluate the following.
(9.9)2
Using suitable identities, evaluate the following.
9.8 × 10.2
Using suitable identities, evaluate the following.
10.1 × 10.2
Using suitable identities, evaluate the following.
(35.4)2 – (14.6)2
Using suitable identities, evaluate the following.
(69.3)2 – (30.7)2
Using suitable identities, evaluate the following.
(9.7)2 – (0.3)2
Using suitable identities, evaluate the following.
(132)2 – (68)2
Using suitable identities, evaluate the following.
(339)2 – (161)2
Using suitable identities, evaluate the following.
(729)2 – (271)2
Write the greatest common factor in the following terms.
–18a2, 108a
Write the greatest common factor in the following terms.
3x2y, 18xy2, – 6xy
Write the greatest common factor in the following terms.
2xy, –y2, 2x2y
Write the greatest common factor in the following terms.
l2m2n, lm2n2, l2mn2
Write the greatest common factor in the following terms.
21pqr, –7p2q2r2, 49p2qr
Write the greatest common factor in the following terms.
qrxy, pryz, rxyz
Write the greatest common factor in the following terms.
3x3y2z, – 6xy3z2, 12x2yz3
Write the greatest common factor in the following terms.
63p2a2r2s, – 9pq2r2s2, 15p2qr2s2, – 60p2a2rs2
Write the greatest common factor in the following terms.
13x2y, 169xy
Write the greatest common factor in the following terms.
11x2, 12y2
Factorise the following expression.
6ab + 12bc
Factorise the following expression.
– xy – ay
Factorise the following expression.
ax3 – bx2 + cx
Factorise the following expression.
l2m2n – lm2n2 – l2mn2
Factorise the following expression.
3pqr – 6p2q2r2 – 15r2
Factorise the following expression.
x3y2 + x2y3 – xy4 + xy
Factorise the following expression.
4xy2 – 10x2y + 16x2y2 + 2xy
Factorise the following expression.
2a3 – 3a2b + 5ab2 – ab
Factorise the following expression.
63p2q2r2s – 9pq2r2s2 + 15p2qr2s2 – 60p2q2rs2
Factorise the following expression.
24x2yz3 – 6xy3z2 + 15x2y2z – 5xyz
Factorise the following expression.
a3 + a2 + a + 1
Factorise the following expression.
lx + my + mx + ly
Factorise the following expression.
a3x – x4 + a2x2 – ax3
Factorise the following expression.
2x2 – 2y + 4xy – x
Factorise the following expression.
y2 + 8zx – 2xy – 4yz
Factorise the following expression.
ax2y – bxyz – ax2z + bxy2
Factorise the following expression.
a2b + a2c + ab + ac + b2c + c2b
Factorise the following expression.
2ax2 + 4axy + 3bx2 + 2ay2 + 6bxy + 3by2
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
x2 + 6x + 9
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
x2 + 12x + 36
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
x2 + 14x + 49
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
x2 + 2x + 1
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
4x2 + 4x + 1
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
a2x2 + 2ax + 1
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
a2x2 + 2abx + b2
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
a2x2 + 2abxy + b2y2
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
4x2 + 12x + 9
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
16x2 + 40x + 25
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
9x2 + 24x + 16
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
9x2 + 30x + 25
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
2x3 + 24x2 + 72x
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
a2x3 + 2abx2 + b2x
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
4x4 + 12x3 + 9x2
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
`x^2/4 + 2x + 4`
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
`9x^2 + 2xy + y^2/9`
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
x2 – 8x + 16
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
x2 – 10x + 25
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
y2 – 14y + 49
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
p2 – 2p + 1
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
4a2 – 4ab + b2
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
p2y2 – 2py + 1
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
a2y2 – 2aby + b2
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
9x2 – 12x + 4
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
4y2 – 12y + 9
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
`x^2/4 - 2x + 4`
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
a2y3 – 2aby2 + b2y
Factorise the following, using the identity a2 – 2ab + b2 = (a – b)2.
`9y^2 - 4xy + (4x^2)/9`
Factorise the following.
x2 + 15x + 26
Factorise the following.
x2 + 9x + 20
Factorise the following.
y2 + 18x + 65
Factorise the following.
p2 + 14p + 13
Factorise the following.
y2 + 4y – 21
Factorise the following.
y2 – 2y – 15
Factorise the following.
18 + 11x + x2
Factorise the following.
x2 – 10x + 21
Factorise the following.
x2 – 17x + 60
Factorise the following.
x2 + 4x – 77
Factorise the following.
y2 + 7y + 12
Factorise the following.
p2 – 13p – 30
Factorise the following.
a2 – 16p – 80
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
x2 – 9
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
4x2 – 25y2
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
4x2 – 49y2
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
3a2b3 – 27a4b
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
28ay2 – 175ax2
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
9x2 – 1
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
25ax2 – 25a
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
`x^2/9 - y^2/25`
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
`(2p^2)/25 - 32q^2`
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
49x2 – 36y2
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
`y^3 - y/9`
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
`x^2/25 - 625`
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
`x^2/8 - y^2/18`
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
`(4x^2)/9 - (9y^2)/16`
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
`(x^3y)/9 - (xy^3)/16`
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
1331x3y – 11y3x
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
`1/36a^2b^2 - 16/49b^2c^2`
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
a4 – (a – b)4
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
x4 – 1
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
y4 – 625
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
p5 – 16p
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
16x4 – 81
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
x4 – y4
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
y4 – 81
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
16x4 – 625y4
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
(a – b)2 – (b – c)2
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
(x + y)4 – (x – y)4
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
x4 – y4 + x2 – y2
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
8a3 – 2a
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
`x^2 - y^2/100`
Factorise the following using the identity a2 – b2 = (a + b)(a – b).
9x2 – (3y + z)2
The following expression is the area of a rectangle. Find the possible length and breadth of the rectangle.
x2 – 6x + 8
The following expression is the area of a rectangle. Find the possible length and breadth of the rectangle.
x2 – 3x + 2
The following expression is the area of a rectangle. Find the possible length and breadth of the rectangle.
x2 – 7x + 10
The following expression is the area of a rectangle. Find the possible length and breadth of the rectangle.
x2 + 19x – 20
The following expression is the area of a rectangle. Find the possible length and breadth of the rectangle.
x2 + 9x + 20
Carry out the following division:
51x3y2z ÷ 17xyz
Carry out the following division:
76x3yz3 ÷ 19x2y2
Carry out the following division:
17ab2c3 ÷ (–abc2)
Carry out the following division:
–121p3q3r3 ÷ (–11xy2z3)
Perform the following division:
(3pqr – 6p2q2r2) ÷ 3pq
Perform the following division:
(ax3 – bx2 + cx) ÷ (– dx)
Perform the following division:
(x3y3 + x2y3 – xy4 + xy) ÷ xy
Perform the following division:
(– qrxy + pryz – rxyz) ÷ (– xyz)
Factorise the expression and divide them as directed:
(x2 – 22x + 117) ÷ (x – 13)
Factorise the expression and divide them as directed:
(x3 + x2 – 132x) ÷ x(x – 11)
Factorise the expression and divide them as directed:
(2x3 – 12x2 + 16x) ÷ (x – 2)(x – 4)
Factorise the expression and divide them as directed:
(9x2 – 4) ÷ (3x + 2)
Factorise the expression and divide them as directed:
(3x2 – 48) ÷ (x – 4)
Factorise the expressions and divide them as directed:
(x4 – 16) ÷ x3 + 2x2 + 4x + 8
Factorise the expression and divide them as directed:
(3x4 – 1875) ÷ (3x2 – 75)
The area of a square is given by 4x2 + 12xy + 9y2. Find the side of the square.
The area of a square is 9x2 + 24xy + 16y2. Find the side of the square.
The area of a rectangle is x2 + 7x + 12. If its breadth is (x + 3), then find its length.
The curved surface area of a cylinder is 2π(y2 – 7y + 12) and its radius is (y – 3). Find the height of the cylinder (C.S.A. of cylinder = 2πrh).
The area of a circle is given by the expression πx2 + 6πx + 9π. Find the radius of the circle.
The sum of first n natural numbers is given by the expression `n^2/2 + n/2`. Factorise this expression.
The sum of (x + 5) observations is x4 – 625. Find the mean of the observations.
The height of a triangle is x4 + y4 and its base is 14xy. Find the area of the triangle.
The cost of a chocolate is Rs (x + y) and Rohit bought (x + y) chocolates. Find the total amount paid by him in terms of x. If x = 10, find the amount paid by him.
The base of a parallelogram is (2x + 3 units) and the corresponding height is (2x – 3 units). Find the area of the parallelogram in terms of x. What will be the area of parallelogram of x = 30 units?
The radius of a circle is 7ab – 7bc – 14ac. Find the circumference of the circle. `(pi = 22/7)`
If p + q = 12 and pq = 22, then find p2 + q2.
If a + b = 25 and a2 + b2 = 225, then find ab.
If x – y = 13 and xy = 28, then find x2 + y2.
If m – n = 16 and m2 + n2 = 400, then find mn.
If a2 + b2 = 74 and ab = 35, then find a + b.
Verify the following:
(ab + bc)(ab – bc) + (bc + ca)(bc – ca) + (ca + ab)(ca – ab) = 0
Verify the following:
(a + b + c)(a2 + b2 + c2 – ab – bc – ca) = a3 + b3 + c3 – 3abc
Verify the following:
(p – q)(p2 + pq + q2) = p3 – q3
Verify the following:
(m + n)(m2 – mn + n2) = m3 + n3
Verify the following:
(a + b)(a + b)(a + b) = a3 + 3a2b + 3ab2 + b3
Verify the following:
(a – b)(a – b)(a – b) = a3 – 3a2b + 3ab2 – b3
Verify the following:
(a2 – b2)(a2 + b2) + (b2 – c2)(b2 + c2) + (c2 – a2) + (c2 + a2) = 0
Verify the following:
(5x + 8)2 – 160x = (5x – 8)2
Verify the following:
(7p – 13q)2 + 364pq = (7p + 13q)2
Verify the following:
`((3p)/7 + 7/(6p))^2 - (3/7p + 7/(6p))^2 = 2`
Find the value of a, if 8a = 352 – 272
Find the value of a, if 9a = 762 – 672
Find the value of a, if pqa = (3p + q)2 – (3p – q)2
Find the value of a, if pq2a = (4pq + 3q)2 – (4pq – 3q)2
What should be added to 4c(– a + b + c) to obtain 3a(a + b + c) – 2b(a – b + c)?
Subtract b(b2 + b – 7) + 5 from 3b2 – 8 and find the value of expression obtained for b = – 3.
If `x - 1/x = 7` then find the value of `x^2 + 1/x^2`.
Factorise `x^2 + 1/x^2 + 2 - 3x - 3/x`.
Factorise p4 + q4 + p2q2.
Find the value of `(6.25 xx 6.25 - 1.75 xx 1.75)/(4.5)`
Find the value of `(198 xx 198 - 102 xx 102)/96`
The product of two expressions is x5 + x3 + x. If one of them is x2 + x + 1, find the other.
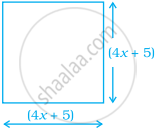
Find the length of the side of the given square if area of the square is 625 square units and then find the value of x.
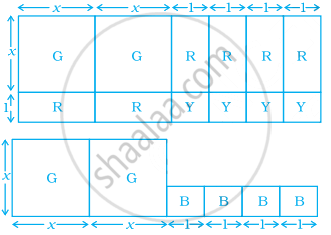
Take suitable number of cards given in the adjoining diagram [G(x × x) representing x2, R(x × 1) representing x and Y(1 × 1) representing 1] to factorise the following expressions, by arranging the cards in the form of rectangles:
- 2x2 + 6x + 4
- x2 + 4x + 4.
Factorise 2x2 + 6x + 4 by using the figure.
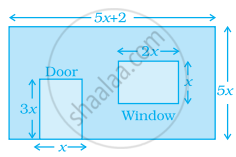
Calculate the area of figure.
The figure shows the dimensions of a wall having a window and a door of a room. Write an algebraic expression for the area of the wall to be painted.
Match the expressions of column I with that of column II:
| Column I | Column II |
| (1) (21x + 13y)2 | (a) 441x2 – 169y2 |
| (2) (21x – 13y)2 | (b) 441x2 + 169y2 + 546xy |
| (3) (21x – 13y)(21x + 13y) | (c) 441x2 + 169y2 – 546xy |
| (d) 441x2 – 169y2 + 546xy |
Solutions for 7: Algebraic Expression, Identities and Factorisation
![NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 7 - Algebraic Expression, Identities and Factorisation NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 7 - Algebraic Expression, Identities and Factorisation - Shaalaa.com](/images/mathematics-english-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 7 - Algebraic Expression, Identities and Factorisation
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 8 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 8 CBSE 7 (Algebraic Expression, Identities and Factorisation) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 8 chapter 7 Algebraic Expression, Identities and Factorisation are Algebraic Expressions, Terms, Factors and Coefficients of Expression, Addition of Algebraic Expressions, Multiplication of Algebraic Expressions, Multiplying Monomial by Monomials, Multiplying a Monomial by a Binomial, Like and Unlike Terms, Subtraction of Algebraic Expressions, Multiplying a Monomial by a Trinomial, Multiplying a Binomial by a Binomial, Multiplying a Binomial by a Trinomial, Concept of Identity, Expansion of (a + b)2 = a2 + 2ab + b2, Expansion of (a - b)2 = a2 - 2ab + b2, Expansion of (a + b)(a - b) = a2-b2, Expansion of (x + a)(x + b), Types of Algebraic Expressions as Monomials, Binomials, Trinomials, and Polynomials, Factors and Multiples, Factorisation by Taking Out Common Factors, Factorising Algebraic Expressions, Factorisation by Regrouping Terms, Factorisation Using Identities, Factors of the Form (x + a)(x + b), Dividing a Monomial by a Monomial, Dividing a Polynomial by a Monomial, Dividing a Polynomial by a Polynomial, Concept of Find the Error.
Using NCERT Exemplar Mathematics [English] Class 8 solutions Algebraic Expression, Identities and Factorisation exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 8 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 7, Algebraic Expression, Identities and Factorisation Mathematics [English] Class 8 additional questions for Mathematics Mathematics [English] Class 8 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
