Advertisements
Advertisements
Question
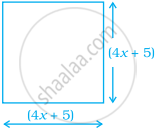
Find the length of the side of the given square if area of the square is 625 square units and then find the value of x.
Solution
We have, a square having length of a side (4x + 5) units and area is 625 sq.units.
∵ Area of a square = (Side)2
(4x + 5)2 = 625
⇒ (4x + 5)2 = (25)2 ...[Taking square root both sides and neglecting (– ve) sign]
⇒ 4x + 5 = 25
⇒ 4x = 25 – 5
⇒ 4x = 20
⇒ x = 5
Hence, side = 4x + 5 = 4 × 5 + 5 = 25 units
APPEARS IN
RELATED QUESTIONS
Use a suitable identity to get the following products.
(7a − 9b) (7a − 9b)
Using a2 − b2 = (a + b) (a − b), find 1532 − 1472
Using (x + a) (x + b) = x2 + (a + b) x + ab, find 103 × 98
Use an expansion formula to find the value.
(97)2
Use the formula to find the value.
97 × 103
`(("a" + "b")("a"^3 - "b"^3))/(("a"^2 - "b"^2))` = ___________
(a + b)2 – 2ab = ______ + ______.
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
4x2 + 12x + 9
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
4x4 + 12x3 + 9x2
Factorise `x^2 + 1/x^2 + 2 - 3x - 3/x`.
