Advertisements
Advertisements
Question
The area of a circle is given by the expression πx2 + 6πx + 9π. Find the radius of the circle.
Solution
We have,
Area of a circle = πx2 + 6πx + 9π = π(x2 + 6x + 9)
⇒ πr2 = π(x2 + 3x + 3x + 9) ...[∵ Area of a circle = πr2, where r is the radius]
⇒ πr2 = π[x(x + 3) + 3(x + 3)] = π(x + 3)(x + 3) = π(x + 3)2
⇒ πr2 = π(x + 3)2
On comapring both sides, r2 = (x + 3)2 ⇒ r = x + 3
Hence, the radius of circle is x + 3.
APPEARS IN
RELATED QUESTIONS
Find the following squares by suing the identities.
(b − 7)2
Find the following squares by suing the identities
(0.4p − 0.5q)2
Using identities, evaluate 297 × 303
Expand (5a + 6b)2
Use a formula to multiply of (2a – 13)(2a + 13)
Expand: (2x + 3y)2
If a + b = 10 and ab = 18, find the value of a2 + b2
Factorise the following, using the identity a2 + 2ab + b2 = (a + b)2.
x2 + 14x + 49
If a2 + b2 = 74 and ab = 35, then find a + b.
Take suitable number of cards given in the adjoining diagram [G(x × x) representing x2, R(x × 1) representing x and Y(1 × 1) representing 1] to factorise the following expressions, by arranging the cards in the form of rectangles: x2 + 4x + 4. Factorise 2x2 + 6x + 4 by using the figure.
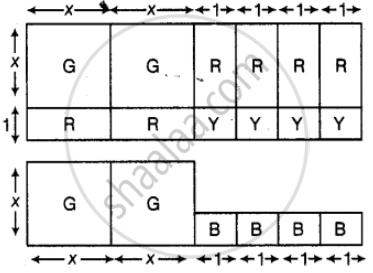
Calculate the area of figure.
