Advertisements
Chapters
2: Data Handling
3: Square-Square Root and Cube-Cube Root
4: Linear Equation In One Variable
5: Understanding Quadrilaterals and Practical Geometry
6: Visualising Solid Shapes
7: Algebraic Expression, Identities and Factorisation
8: Exponents and Powers
9: Comparing Quantities
10: Direct and Inverse Proportions
11: Mensuration
12: Introduct To Graphs
13: Playing With Numbers
![NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 1 - Rational Numbers NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 1 - Rational Numbers - Shaalaa.com](/images/mathematics-english-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 1: Rational Numbers
Below listed, you can find solutions for Chapter 1 of CBSE NCERT Exemplar for Mathematics [English] Class 8.
NCERT Exemplar solutions for Mathematics [English] Class 8 1 Rational Numbers Exercise [Pages 9 - 27]
Choose the correct alternative:
A number which can be expressed as `p/q` where p and q are integers and q ≠ 0 is ______
natural number.
whole number.
integer.
rational number.
A number of the form `p/q` is said to be a rational number if ______.
p and q are integers
p and q are integers and q ≠ 0
p and q are integers and p ≠ 0
p and q are integers and p ≠ 0 also q ≠ 0
The numerical expression `3/8 + ((-5))/7 = (-19)/56` shows that ______
rational numbers are closed under addition.
rational numbers are not closed under addition.
rational numbers are closed under multiplication.
addition of rational numbers is not commutative.
Which of the following is not true?
Rational numbers are closed under addition.
Rational numbers are closed under subtraction.
Rational numbers are closed under multiplication.
Rational numbers are closed under division.
`- 3/8 + 1/7 = 1/7 + ((-3)/8)` is an example to show that ______
addition of rational numbers is commutative.
rational numbers are closed under addition.
addition of rational number is associative.
rational numbers are distributive under addition.
Which of the following expressions shows that rational numbers are associative under multiplication?
`2/3 xx ((-6)/7 xx 3/5) = (2/3 xx (-6)/7) xx 3/5`
`2/3 xx ((-6)/7 xx 3/5) = 2/3 xx (3/5 xx (-6)/7)`
`2/3 xx ((-6)/7 xx 3/5) = (3/5 xx 2/3) xx (-6)/7`
`(2/3 xx (-6)/7) xx 3/5 = ((-6)/7 xx 2/3) xx 3/5`
Zero (0) is ______
the identity for addition of rational numbers.
the identity for subtraction of rational numbers.
the identity for multiplication of rational numbers.
the identity for division of rational numbers.
One (1) is ______
the identity for addition of rational numbers.
the identity for subtraction of rational numbers.
the identity for multiplication of rational numbers.
the identity for division of rational numbers.
The additive inverse of `(-7)/19` is ______.
`(-7)/19`
`7/19`
`19/7`
`(-19)/7`
Multiplicative inverse of a negative rational number is ______
a positive rational number.
a negative rational number.
0
1
If x + 0 = 0 + x = x, which is rational number, then 0 is called ______
identity for addition of rational numbers.
additive inverse of x.
multiplicative inverse of x.
reciprocal of x.
To get the product 1, we should multiply `8/21` by ______.
`8/21`
`(-8)/21`
`21/8`
`(-21)/8`
– (–x) is same as ______.
– x
x
`1/x`
`(-1)/x`
The multiplicative inverse of `-1 1/7` is ______.
`8/7`
`(-8)/7`
`7/8`
`7/(-8)`
If x be any rational number then x + 0 is equal to ______.
x
0
– x
Not defined
The reciprocal of 1 is ______.
1
–1
0
Not defined
The reciprocal of –1 is ______.
1
–1
0
Not defined
The reciprocal of 0 is ______.
1
–1
0
Not defined
The reciprocal of any rational number `p/q`, where p and q are integers and q ≠ 0, is ______.
`p/q`
1
0
`q/p`
If y be the reciprocal of rational number x, then the reciprocal of y will be ______.
x
y
`x/y`
`y/x`
The reciprocal of `(-3)/8 xx ((-7)/13)` is ______.
`104/21`
`(-104)/21`
`21/104`
`(-21)/104`
Which of the following is an example of distributive property of multiplication over addition for rational numbers?
`-1/4 xx {2/3 + ((-4)/7)} = [-1/4 xx 2/3] + [-1/4 xx ((-4)/7)]`
`-1/4 xx {2/3 + ((-4)/7)} = [1/4 xx 2/3] - ((-4)/7)`
`-1/4 xx {2/3 + ((-4)/7)} = 2/3 + (-1/4) xx (-4)/7`
`-1/4 xx {2/3 + ((-4)/7)} = {2/3 + ((-4)/7)} - 1/4`
Between two given rational numbers, we can find ______
one and only one rational number.
only two rational numbers.
only ten rational numbers.
infinitely many rational numbers.
`(x + y)/2` is a rational number.
Between x and y
Less than x and y both.
Greater than x and y both.
Less than x but greater than y.
Which of the following statements is always true?
`(x - y)/2` is a rational number between x and y.
`(x + y)/2` is a rational number between x and y.
`(x xx y)/2` is a rational number between x and y.
`(x ÷ y)/2` is a rational number between x and y.
Fill in the blanks:
The equivalent of `5/7`, whose numerator is 45 is ______.
The equivalent rational number of `7/9`, whose denominator is 45 is ______.
Between the numbers `15/20` and `35/40`, the greater number is ______.
The reciprocal of a positive rational number is ______.
The reciprocal of a negative rational number is ______.
Zero has ______ reciprocal.
The numbers ______ and ______ are their own reciprocal.
If y be the reciprocal of x, then the reciprocal of y2 in terms of x will be ______.
The reciprocal of `2/5 xx ((-4)/9)` is ______.
(213 × 657)–1 = 213–1 × ______.
The negative of 1 is ______.
For rational numbers `a/b, c/d` and `e/f` we have `a/b xx (c/d + e/f)` = ______ + ______.
`(-5)/7` is ______ than –3.
There are ______ rational numbers between any two rational numbers.
The rational numbers `1/3` and `(-1)/3`are on the ______ sides of zero on the number line.
The negative of a negative rational number is always a ______ rational number.
Rational numbers can be added or multiplied in any ______.
The reciprocal of `(-5)/7` is ______.
The multiplicative inverse of `4/3` is ______.
The rational number 10.11 in the from `p/q` is ______.
`1/5 xx [2/7 + 3/8] = [1/5 xx 2/7] +` ______.
The two rational numbers lying between –2 and –5 with denominator as 1 are ______ and ______.
State whether the following statement is True or False:
If `x/y` is a rational number, then y is always a whole number.
True
False
If `p/q` is a rational number, then p cannot be equal to zero.
True
False
If `r/s` is a rational number, then s cannot be equal to zero.
True
False
`5/6` lies between `2/3` and 1.
True
False
`5/10` lies between `1/2` and 1.
True
False
`(-7)/2` lies between –3 and –4.
True
False
`9/6` lies between 1 and 2.
True
False
If a ≠ 0, the multiplicative inverse of `a/b` is `b/a`.
True
False
The multiplicative inverse of `(-3)/5` is `5/3`.
True
False
The additive inverse of `1/2` is –2.
True
False
If `x/y` is the additive inverse of `c/d`, then `x/y + c/d` = 0.
True
False
For every rational number x, x + 1 = x.
True
False
If `x/y` is the additive inverse of `c/d`, then `x/y - c/d = 0`
True
False
The reciprocal of a non-zero rational number `q/p` is the rational number `q/p`.
True
False
If x + y = 0, then –y is known as the negative of x, where x and y are rational numbers.
True
False
The negative of the negative of any rational number is the number itself.
True
False
The negative of 0 does not exist.
True
False
The negative of 1 is 1 itself.
True
False
For all rational numbers x and y, x – y = y – x.
True
False
For all rational numbers x and y, x × y = y × x.
True
False
For every rational number x, x × 0 = x.
True
False
For every rational numbers x, y and z, x + (y × z) = (x + y) × (x + z).
True
False
For all rational numbers a, b and c, a(b + c) = ab + bc.
True
False
1 is the only number which is its own reciprocal.
True
False
–1 is not the reciprocal of any rational number.
True
False
For any rational number x, x + (–1) = –x.
True
False
For rational numbers x and y, if x < y then x – y is a positive rational number.
True
False
If x and y are negative rational numbers, then so is x + y.
True
False
Between any two rational numbers there are exactly ten rational numbers.
True
False
Rational numbers are closed under addition and multiplication but not under subtraction.
True
False
Subtraction of rational number is commutative.
True
False
`-3/4` is smaller than –2.
True
False
0 is a rational number.
True
False
All positive rational numbers lie between 0 and 1000.
True
False
The population of India in 2004 - 05 is a rational number.
True
False
There are countless rational numbers between `5/6` and `8/9`.
True
False
The reciprocal of x–1 is `1/x`.
True
False
The rational number `57/23` lies to the left of zero on the number line.
True
False
The rational number `7/(-4)` lies to the right of zero on the number line.
True
False
The rational number `(-8)/(-3)` lies neither to the right nor to the left of zero on the number line.
True
False
The rational numbers `1/2` and –1 are on the opposite sides of zero on the number line.
True
False
Every fraction is a rational number.
True
False
Every integer is a rational number.
True
False
The rational numbers can be represented on the number line.
True
False
The negative of a negative rational number is a positive rational number.
True
False
If x and y are two rational numbers such that x > y, then x – y is always a positive rational number.
True
False
0 is the smallest rational number.
True
False
Every whole number is an integer.
True
False
Every whole number is a rational number.
True
False
0 is whole number but it is not a rational number.
True
False
The rational numbers `1/2` and `- 5/2` are on the opposite sides of 0 on the number line.
True
False
Rational numbers can be added (or multiplied) in any order
`(-4)/5 xx (-6)/5 = (-6)/5 xx (-4)/5`
True
False
Solve the following: Select the rational numbers from the list which are also the integers.
`9/4, 8/4, 7/4, 6/4, 9/3, 8/3, 7/3, 6/3, 5/2, 4/2, 3/1, 3/2, 1/1, 0/1, (-1)/1, (-2)/1, (-3)/2, (-4)/2, (-5)/2, (-6)/2`
Select those which can be written as a rational number with denominator 4 in their lowest form:
`7/8, 64/16, 36/(-12), (-16)/17, 5/(-4), 140/28`
Using suitable rearrangement and find the sum:
`4/7 + ((-4)/9) + 3/7 + ((-13)/9)`
Using suitable rearrangement and find the sum:
`-5 + 7/10 + 3/7 + (-3) + 5/14 + (-4)/5`
Verify – (– x) = x for x = `3/5`
Verify – (– x) = x for x = `(-7)/9`
Verify – (– x) = x for x = `13/(-15)`
Give one example each to show that the rational numbers are closed under addition, subtraction and multiplication. Are rational numbers closed under division? Give two examples in support of your answer.
Verify the property x + y = y + x of rational numbers by taking
`x = 1/2, y = 1/2`
Verify the property x + y = y + x of rational numbers by taking
`x = (-2)/3, y = (-5)/6`
Verify the property x + y = y + x of rational numbers by taking
`x = (-3)/7, y = 20/21`
Verify the property x + y = y + x of rational numbers by taking
`x = (-2)/5, y = (-9)/10`
Simplify the following by using suitable property. Also name the property.
`[1/2 xx 1/4] + [1/2 xx 6]`
Simplify the following by using suitable property. Also name the property.
`[1/5 xx 2/15] - [1/5 xx 2/5]`
Simplify the following by using suitable property. Also name the property.
`(-3)/5 xx {3/7 + ((-5)/6)}`
Tell which property allows you to compute `1/5 xx [5/6 xx 7/9]` as `[1/5 xx 5/6] xx 7/9`
Verify the property x × y = y × x of rational numbers by using
`x = 7` and `y = 1/2`
Verify the property x × y = y × x of rational numbers by using
`x = 2/3` and `y = 9/4`
Verify the property x × y = y × x of rational numbers by using
`x = (-5)/7` and `y = 14/15`
Verify the property x × y = y × x of rational numbers by using
`x = (-3)/8` and `y = (-4)/9`
Verify the property x × (y × z) = (x × y) × z of rational numbers by using
`x = 1, y = (-1)/2` and `z = 1/4`
and What is the name of this property?
Verify the property x × (y × z) = (x × y) × z of rational numbers by using
`x = 2/3, y = (-3)/7` and `z = 1/2`
and What is the name of this property?
Verify the property x × (y × z) = (x × y) × z of rational numbers by using
`x = (-2)/7, y = (-5)/6` and `z = 1/4`
and What is the name of this property?
Verify the property x × (y × z) = (x × y) × z of rational numbers by using
`x = 0, y = 1/2` and `z = 1/4`
and What is the name of this property?
Verify the property x × (y + z) = x × y + x × z of rational numbers by taking.
`x = (-1)/2, y = 3/4, z = 1/4`
Verify the property x × (y + z) = x × y + x × z of rational numbers by taking.
`x = (-1)/2, y = 2/3, z = 3/4`
Verify the property x × (y + z) = x × y + x × z of rational numbers by taking.
`x = (-2)/3, y = (-4)/6, z = (-7)/9`
Verify the property x × (y + z) = x × y + x × z of rational numbers by taking.
`x = (-1)/5, y = 2/15, z = (-3)/10`
Use the distributivity of multiplication of rational numbers over their addition to simplify:
Use the distributivity of multiplication of rational numbers over their addition to simplify:
Use the distributivity of multiplication of rational numbers over their addition to simplify:
Use the distributivity of multiplication of rational numbers over their addition to simplify:
Simplify
`32/5 + 23/11 xx 22/15`
Simplify
`3/7 xx 28/15 ÷ 14/5`
Simplify
`3/7 + (-2)/21 xx (-5)/6`
Simplify
`7/8 + 1/16 - 1/12`
Identify the rational number that does not belong with the other three. Explain your reasoning
`(-5)/11, (-1)/2, (-4)/9, (-7)/3`
The cost of `19/4` metres of wire is Rs. `171/2`. Find the cost of one metre of the wire.
A train travels `1445/2` km in `17/2` hours. Find the speed of the train in km/h.
If 16 shirts of equal size can be made out of 24 m of cloth, how much cloth is needed for making one shirt?
`7/11` of all the money in Hamid’s bank account is Rs. 77,000. How much money does Hamid have in his bank account?
A `117 1/3` m long rope is cut into equal pieces measuring `7 1/3` m each. How many such small pieces are these?
`1/6` of the class students are above average, `1/4` are average and rest are below average. If there are 48 students in all, how many students are below average in the class?
`2/5` of total number of students of a school come by car while `1/4` of students come by bus to school. All the other students walk to school of which `1/3` walk on their own and the rest are escorted by their parents. If 224 students come to school walking on their own, how many students study in that school?
Huma, Hubna and Seema received a total of Rs. 2,016 as monthly allowance from their mother such that Seema gets `1/2` of what Huma gets and Hubna gets `1 2/3` times Seema’s share. How much money do the three sisters get individually?
A mother and her two daughters got a room constructed for Rs. 62,000. The elder daughter contributes `3/8` of her mother’s contribution while the younger daughter contributes `1/2` of her mother’s share. How much do the three contribute individually?
Tell which property allows you to compare
`2/3 xx [3/4 xx 5/7]` and `[2/3 xx 5/7] xx 3/4`
Name the property used in the following.
`-7/11 xx (-3)/5 = (-3)/5 xx (-7)/11`
Name the property used in the following.
`-2/3 xx [3/4 + (-1)/2] = [(-2)/3 xx 3/4] + [(-2)/3 xx (-1)/2]`
Name the property used in the following.
`1/3 + [4/9 + ((-4)/3)] = [1/3 + 4/9] + [(-4)/3]`
Name the property used in the following.
`(-2)/7 + 0 = 0 + (-2)/7 = - 2/7`
Name the property used in the following.
`3/8 xx 1 = 1 xx 3/8 = 3/8`
Find the multiplicative inverse of `-1 1/8`
Find the multiplicative inverse of `3 1/3`
Arrange the numbers `1/4, 13/16, 5/8` in the descending order.
The product of two rational numbers is `(-14)/27`. If one of the numbers be `7/9`, find the other.
By what numbers should we multiply `(-15)/20` so that the product may be `(-5)/7`?
By what number should we multiply `(-8)/13` so that the product may be 24?
The product of two rational numbers is –7. If one of the number is –5, find the other?
Can you find a rational number whose multiplicative inverse is –1?
Find five rational numbers between 0 and 1.
Find two rational numbers whose absolute value is `1/5`.
From a rope 40 metres long, pieces of equal size are cut. If the length of one piece is `10/3` metre, find the number of such pieces.
`5 1/2` metres long rope is cut into 12 equal pieces. What is the length of each piece?
Write the following rational numbers in the descending order.
`8/7, (-9)/8, (-3)/2, 0, 2/5`
Find `0 ÷ 2/3`
Find `1/3 xx (-5)/7 xx (-21)/10`
On a winter day the temperature at a place in Himachal Pradesh was –16°C. Convert it in degree Fahrenheit (°F) by using the formula.
`C/5 = (F - 32)/9`
Find the sum of additive inverse and multiplicative inverse of 7.
Find the product of additive inverse and multiplicative inverse of `- 1/3`.
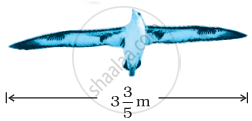
The diagram shows the wingspans of different species of birds. Use the diagram to answer the question given below:
| Albatross | Sea Gull |
 |
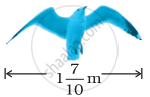 |
How much longer is the wingspan of an Albatross than the wingspan of a Sea gull?
The diagram shows the wingspans of different species of birds. Use the diagram to answer the question given below:
| Golden eagle | Blue jay |
 |
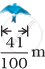 |
How much longer is the wingspan of a Golden eagle than the wingspan of a Blue jay?
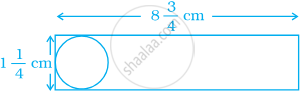
Shalini has to cut out circles of diameter `1 1/4` cm from an aluminium strip of dimensions `8 3/4` cm by `1 1/4` cm. How many full circles can Shalini cut? Also calculate the wastage of the aluminium strip.
One fruit salad recipe requires `1/2` cup of sugar. Another recipe for the same fruit salad requires 2 tablespoons of sugar. If 1 tablespoon is equivalent to `1/16` cup, how much more sugar does the first recipe require?
Four friends had a competition to see how far could they hop on one foot. The table given shows the distance covered by each.
| Name | Distance covered (km) |
| Seema | `1/25` |
| Nancy | `1/32` |
| Megha | `1/40` |
| Soni | `1/20` |
- How farther did Soni hop than Nancy?
- What is the total distance covered by Seema and Megha?
- Who walked farther, Nancy or Megha?
The table given below shows the distances, in kilometres, between four villages of a state. To find the distance between two villages, locate the square where the row for one village and the column for the other village intersect.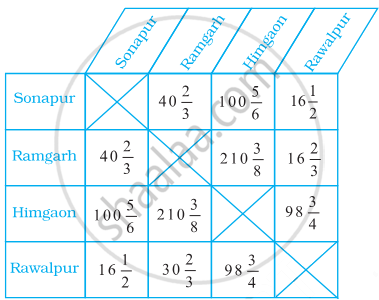
Compare the distance between Himgaon and Rawalpur to Sonapur and Ramgarh?
The table given below shows the distances, in kilometres, between four villages of a state. To find the distance between two villages, locate the square where the row for one village and the column for the other village intersect.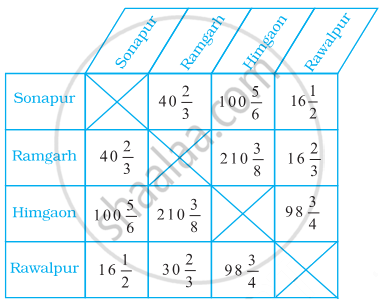
If you drove from Himgaon to Sonapur and then from Sonapur to Rawalpur, how far would you drive?
The table shows the portion of some common materials that are recycled.
| Material | Recycled |
| Paper | `5/11` |
| Aluminium cans | `5/8` |
| Glass | `2/5` |
| Scrap | `3/4` |
- Is the rational number expressing the amount of paper recycled more than `1/2` or less than `1/2`?
- Which items have a recycled amount less than `1/2`?
- Is the quantity of aluminium cans recycled more (or less) than half of the quantity of aluminium cans?
- Arrange the rate of recycling the materials from the greatest to the smallest.
The overall width in cm of several wide-screen televisions are 97.28 cm, `98 4/9` cm `98 1/25` cm and 97.94 cm. Express these numbers as rational numbers in the form `p/q` and arrange the widths in ascending order.
Roller Coaster at an amusement park is `2/3` m high. If a new roller coaster is built that is `3/5` times the height of the existing coaster, what will be the height of the new roller coaster?
Here is a table which gives the information about the total rainfall for several months compared to the average monthly rains of a town. Write each decimal in the form of rational number `p/q`.
| Month | Above/Below normal (in cm) |
| May | 2.6924 |
| June | 0.6096 |
| July | – 6.9088 |
| August | – 8.636 |
The average life expectancies of males for several states are shown in the table. Express each decimal in the form `p/q` and arrange the states from the least to the greatest male life expectancy. State-wise data are included below; more indicators can be found in the “FACTFILE” section on the homepage for each state.
| State | Male | `bb(p/q)` form | Lowest terms |
| Andhra Pradesh | 61.6 | ||
| Assam | 57.1 | ||
| Bihar | 60.7 | ||
| Gujarat | 61.9 | ||
| Haryana | 64.1 | ||
| Himachal Pradesh | 65.1 | ||
| Karnataka | 62.4 | ||
| Kerala | 70.6 | ||
| Madhya Pradesh | 56.5 | ||
| Maharashtra | 64.5 | ||
| Orissa | 57.6 | ||
| Punjab | 66.9 | ||
| Rajasthan | 59.8 | ||
| Tamil Nadu | 63.7 | ||
| Uttar Pradesh | 58.9 | ||
| West Bengal | 62.8 | ||
| India | 60.8 |
Source: Registrar General of India (2003) SRS Based Abridged Lefe Tables. SRS Analytical Studies, Report No. 3 of 2003, New Delhi: Registrar General of India. The data are for the 1995-99 period; states subsequently divided are therefore included in their pre-partition states (Chhatisgarh in MP, Uttaranchal in UP and Jharkhand in Bihar)
A skirt that is `35 7/8` cm long has a hem of `3 1/8` cm. How long will the skirt be if the hem is let down?
Manavi and Kuber each receives an equal allowance. The table shows the fraction of their allowance each deposits into his/her saving account and the fraction each spends at the mall. If allowance of each is Rs. 1260 find the amount left with each.
| Where money goes | Fraction of allowance | |
| Manavi | Kuber | |
| Saving Account | `1/2` | `1/3` |
| Spend at mall | `1/4` | `3/5` |
| Left over | ? | ? |
Solutions for 1: Rational Numbers
![NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 1 - Rational Numbers NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 1 - Rational Numbers - Shaalaa.com](/images/mathematics-english-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 1 - Rational Numbers
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 8 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 8 CBSE 1 (Rational Numbers) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 8 chapter 1 Rational Numbers are Closure Property of Rational Numbers, Commutative Property of Rational Numbers, Identity of Addition and Multiplication of Rational Numbers, Associative Property of Rational Numbers, Distributive Property of Multiplication Over Addition for Rational Numbers, Rational Numbers Between Two Rational Numbers, Rational Numbers, Negative Or Additive Inverse of Rational Numbers, Concept of Reciprocal or Multiplicative Inverse, Rational Numbers on a Number Line.
Using NCERT Exemplar Mathematics [English] Class 8 solutions Rational Numbers exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 8 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 1, Rational Numbers Mathematics [English] Class 8 additional questions for Mathematics Mathematics [English] Class 8 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
