NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 3 - Square-Square Root and Cube-Cube Root [Latest edition]

196 is the square of ______.

Which of the following is a square of an even number?

A number ending in 9 will have the units place of its square as ______.

Which of the following will have 4 at the units place?

How many natural numbers lie between 5² and 6²?

Which of the following cannot be a perfect square?

The one’s digit of the cube of 23 is ______.

A square board has an area of 144 square units. How long is each side of the board?

Which letter best represents the location of `sqrt(25)` on a number line?

If one member of a pythagorean triplet is 2m, then the other two members are ______.

The sum of successive odd numbers 1, 3, 5, 7, 9, 11, 13 and 15 is ______.

The sum of first n odd natural numbers is ______.

Which of the following numbers is a perfect cube?

The hypotenuse of a right triangle with its legs of lengths 3x × 4x is ______.

The next two numbers in the number pattern 1, 4, 9, 16, 25 ... are ______.

Which among 43², 67², 52², 59² would end with digit 1?

A perfect square can never have the following digit in its ones place.

Which of the following numbers is not a perfect cube?

`root(3)(1000)` is equal to ______.

If m is the square of a natural number n, then n is ______.

A perfect square number having n digits where n is even will have square root with ______.

If m is the cube root of n, then n is ______.

The value of `sqrt(248 + sqrt(52 + sqrt(144)` is ______.

Given that `sqrt(4096) = 64`, the value of `sqrt(4096) + sqrt(40.96)` is ______.

There are ______ perfect squares between 1 and 100.

There are ______ perfect cubes between 1 and 1000.

The units digit in the square of 1294 is ______.

The square of 500 will have ______ zeroes.

There are ______ natural numbers between n² and (n + 1)² 

The square root of 24025 will have ______ digits.

The square of 5.5 is ______.

The square root of 5.3 × 5.3 is ______.

The cube of 100 will have ______ zeroes.

1m² = ______ cm².

1m³ = ______ cm³.

Ones digit in the cube of 38 is ______.

The square of 0.7 is ______.

The sum of first six odd natural numbers is ______.

The digit at the ones place of 57² is ______.

The sides of a right triangle whose hypotenuse is 17 cm are ______ and ______.

`sqrt(1.96)` = ______.

(1.2)³ = ______.

The cube of an odd number is always an ______ number.

The cube root of a number x is denoted by ______.

The least number by which 125 be multiplied to make it a perfect square is ______.

The least number by which 72 be multiplied to make it a perfect cube is ______.

The least number by which 72 be divided to make it a perfect cube is ______.

Cube of a number ending in 7 will end in the digit ______.

The square of 86 will have 6 at the units place.

The sum of two perfect squares is a perfect square.

The product of two perfect squares is a perfect square.

There is no square number between 50 and 60.

The square root of 1521 is 31.

Each prime factor appears 3 times in its cube.

The square of 2.8 is 78.4.

The cube of 0.4 is 0.064.

The square root of 0.9 is 0.3.

The square of every natural number is always greater than the number itself.

The cube root of 8000 is 200.

There are five perfect cubes between 1 and 100.

There are 200 natural numbers between 100² and 101².

The sum of first n odd natural numbers is n².

1000 is a perfect square.

A perfect square can have 8 as its units digit.

For every natural number m, (2m – 1, 2m² – 2m, 2m² – 2m + 1) is a pythagorean triplet.

All numbers of a pythagorean triplet are odd.

For an integer a, a³ is always greater than a².

If x and y are integers such that x² > y², then x³ > y³.

Let x and y be natural numbers. If x divides y, then x³ divides y³.

If a² ends in 5, then a³ ends in 25.

If a² ends in 9, then a³ ends in 7.

The square root of a perfect square of n digits will have `((n + 1)/2)` digits, if n is odd.

Square root of a number x is denoted by `sqrt(x)`.

A number having 7 at its ones place will have 3 at the units place of its square.

A number having 7 at its ones place will have 3 at the ones place of its cube.

The cube of a one-digit number cannot be a two-digit number.

Cube of an even number is odd.

Cube of an odd number is even.

Cube of an even number is even.

Cube of an odd number is odd.

999 is a perfect cube.

363 × 81 is a perfect cube.

Cube roots of 8 are +2 and –2.

`root(3)(8 + 27) = root(3)(8) + root(3)(27)`.

There is no cube root of a negative integer.

Square of a number is positive, so the cube of that number will also be positive.

Write the first five square numbers.

Write cubes of first three multiples of 3.

Show that 500 is not a perfect square.

Express 81 as the sum of first nine consecutive odd numbers.

Using prime factorisation, find which of the following are perfect squares.

484

Using prime factorisation, find which of the following are perfect squares.

11250

Using prime factorisation, find which of the following are perfect squares.

841

Using prime factorisation, find which of the following are perfect squares.

729

Using prime factorisation, find which of the following are perfect cubes.

128

Using prime factorisation, find which of the following are perfect cubes.

343

Using prime factorisation, find which of the following are perfect cubes.

729

Using prime factorisation, find which of the following are perfect cubes.

1331

Using distributive law, find the square of 101

Using distributive law, find the square of 72

Can a right triangle with sides 6 cm, 10 cm and 8 cm be formed? Give reason.

Write the Pythagorean triplet whose one of the numbers is 4.

Using prime factorisation, find the square roots of 11025

Using prime factorisation, find the square roots of 4761

Using prime factorisation, find the cube roots of 512

Using prime factorisation, find the cube roots of 2197

Is 176 a perfect square? If not, find the smallest number by which it should be multiplied to get a perfect square.

Is 9720 a perfect cube? If not, find the smallest number by which it should be divided to get a perfect cube.

Write two Pythagorean triplets each having one of the numbers as 5.

By what smallest number should 216 be divided so that the quotient is a perfect square. Also find the square root of the quotient.

By what smallest number should 3600 be multiplied so that the quotient is a perfect cube. Also find the cube root of the quotient.

Find the square root of the following by long division method.

1369

Find the square root of the following by long division method.

5625

Find the square root of the following by long division method.

27.04

Find the square root of the following by long division method.

1.44

What is the least number that should be subtracted from 1385 to get a perfect square? Also find the square root of the perfect square.

What is the least number that should be added to 6200 to make it a perfect square?

Find the least number of four digits that is a perfect square.

Find the greatest number of three digits that is a perfect square.

Find the least square number which is exactly divisible by 3, 4, 5, 6 and 8.

Find the length of the side of a square if the length of its diagonal is 10 cm.

A decimal number is multiplied by itself. If the product is 51.84, find the number.

Find the decimal fraction which when multiplied by itself gives 84.64.

A farmer wants to plough his square field of side 150 m. How much area will he have to plough?

What will be the number of unit squares on each side of a square graph paper if the total number of unit squares is 256?

If one side of a cube is 15 m in length, find its volume.

The dimensions of a rectangular field are 80 m and 18 m. Find the length of its diagonal.

Find the area of a square field if its perimeter is 96 m.

Find the length of each side of a cube if its volume is 512 cm³.

Three numbers are in the ratio 1 : 2 : 3 and the sum of their cubes is 4500. Find the numbers.

How many square metres of carpet will be required for a square room of side 6.5 m to be carpeted.

Find the side of a square whose area is equal to the area of a rectangle with sides 6.4 m and 2.5 m.

Difference of two perfect cubes is 189. If the cube root of the smaller of the two numbers is 3, find the cube root of the larger number.

Find the number of plants in each row if 1024 plants are arranged so that number of plants in a row is the same as the number of rows.

A hall has a capacity of 2704 seats. If the number of rows is equal to the number of seats in each row, then find the number of seats in each row

A General wishes to draw up his 7500 soldiers in the form of a square. After arranging, he found out that some of them are left out. How many soldiers were left out?

8649 students were sitting in a lecture room in such a manner that there were as many students in the row as there were rows in the lecture room. How many students were there in each row of the lecture room?

Rahul walks 12 m north from his house and turns west to walk 35 m to reach his friend’s house. While returning, he walks diagonally from his friend’s house to reach back to his house. What distance did he walk while returning?

A 5.5 m long ladder is leaned against a wall. The ladder reaches the wall to a height of 4.4 m. Find the distance between the wall and the foot of the ladder.

A king wanted to reward his advisor, a wise man of the kingdom. So he asked the wiseman to name his own reward. The wiseman thanked the king but said that he would ask only for some gold coins each day for a month. The coins were to be counted out in a pattern of one coin for the first day, 3 coins for the second day, 5 coins for the third day and so on for 30 days. Without making calculations, find how many coins will the advisor get in that month?

Find three numbers in the ratio 2 : 3 : 5, the sum of whose squares is 608.

Find the smallest square number divisible by each one of the numbers 8, 9 and 10.

The area of a square plot is `101 1/400`m². Find the length of one side of the plot.

Find the square root of 324 by the method of repeated subtraction.

Three numbers are in the ratio 2 : 3 : 4. The sum of their cubes is 0.334125. Find the numbers.

Evaluate:

`root(3)(27) + root(3)(0.008) + root(3)(0.064)`

Evaluate: 

`{(5^2 + (12^2)^(1/2))}^3`

Evaluate: 

`{(6^2 + (8^2)^(1/2))}^3`

A perfect square number has four digits, none of which is zero. The digits from left to right have values that are: even, even, odd, even. Find the number.

Put three different numbers in the circles so that when you add the numbers at the end of each line you always get a perfect square.

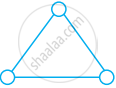
The perimeters of two squares are 40 and 96 metres respectively. Find the perimeter of another square equal in area to the sum of the first two squares.

A three digit perfect square is such that if it is viewed upside down, the number seen is also a perfect square. What is the number?

(Hint: The digits 1, 0 and 8 stay the same when viewed upside down, whereas 9 becomes 6 and 6 becomes 9.)

13 and 31 is a strange pair of numbers such that their squares 169 and 961 are also mirror images of each other. Find two more such pairs.