Advertisements
Advertisements
Question
Find the length of the side of a square if the length of its diagonal is 10 cm.
Solution
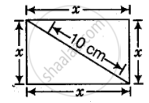
Given, length of diagonal = 10 cm
Suppose, the length of side of a square is x cm.
By using Pythagoras theorem,
(10)2 = x2 + x2
⇒ 100 = 2x2
⇒ x2 = 50
⇒ x = `sqrt(50)` ...[Taking square root on both sides]
∴ x = `5sqrt(2)` cm
Hence, the length of the side of square is `sqrt(50)` or `5sqrt(2)` cm.
APPEARS IN
RELATED QUESTIONS
Observe the following pattern \[1 = \frac{1}{2}\left\{ 1 \times \left( 1 + 1 \right) \right\}\]
\[ 1 + 2 = \frac{1}{2}\left\{ 2 \times \left( 2 + 1 \right) \right\}\]
\[ 1 + 2 + 3 = \frac{1}{2}\left\{ 3 \times \left( 3 + 1 \right) \right\}\]
\[1 + 2 + 3 + 4 = \frac{1}{2}\left\{ 4 \times \left( 4 + 1 \right) \right\}\]
and find the values of following:
1 + 2 + 3 + 4 + 5 + ... + 50
Find the squares of the following numbers using diagonal method:
295
Find the square of the following number:
265
Find the square of the following number:
575
Find the square of the following number:
405
Find the square of the following number:
512
If x and y are integers such that x2 > y2, then x3 > y3.
Write two Pythagorean triplets each having one of the numbers as 5.
Rahul walks 12 m north from his house and turns west to walk 35 m to reach his friend’s house. While returning, he walks diagonally from his friend’s house to reach back to his house. What distance did he walk while returning?
Put three different numbers in the circles so that when you add the numbers at the end of each line you always get a perfect square.