Advertisements
Advertisements
Question
Find the square of the following number:
265
Solution
We will use visual method as it is the most efficient method to solve this problem.
We have:
265 = 260 + 5
Hence, let us draw a square having side 265 units. Let us split it into 260 units and 5 units.
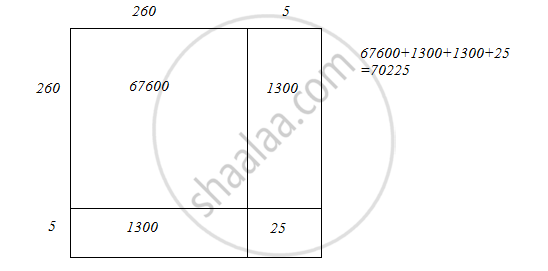
Hence, the square of 265 is 70225.
APPEARS IN
RELATED QUESTIONS
Find the square of the given number.
93
What will be the units digit of the square of the following number?
78367
Observe the following pattern \[1 = \frac{1}{2}\left\{ 1 \times \left( 1 + 1 \right) \right\}\]
\[ 1 + 2 = \frac{1}{2}\left\{ 2 \times \left( 2 + 1 \right) \right\}\]
\[ 1 + 2 + 3 = \frac{1}{2}\left\{ 3 \times \left( 3 + 1 \right) \right\}\]
\[1 + 2 + 3 + 4 = \frac{1}{2}\left\{ 4 \times \left( 4 + 1 \right) \right\}\]and find the values of following:
31 + 32 + ... + 50
Observe the following pattern \[1^2 = \frac{1}{6}\left[ 1 \times \left( 1 + 1 \right) \times \left( 2 \times 1 + 1 \right) \right]\]
\[ 1^2 + 2^2 = \frac{1}{6}\left[ 2 \times \left( 2 + 1 \right) \times \left( 2 \times 2 + 1 \right) \right]\]
\[ 1^2 + 2^2 + 3^2 = \frac{1}{6}\left[ 3 \times \left( 3 + 1 \right) \times \left( 2 \times 3 + 1 \right) \right]\]
\[ 1^2 + 2^2 + 3^2 + 4^2 = \frac{1}{6}\left[ 4 \times \left( 4 + 1 \right) \times \left( 2 \times 4 + 1 \right) \right]\] and find the values :
52 + 62 + 72 + 82 + 92 + 102 + 112 + 122
Find the square of the following number:
995
The hypotenuse of a right triangle with its legs of lengths 3x × 4x is ______.
If m is the square of a natural number n, then n is ______.
Write the Pythagorean triplet whose one of the numbers is 4.
Write two Pythagorean triplets each having one of the numbers as 5.
The dimensions of a rectangular field are 80 m and 18 m. Find the length of its diagonal.
