Advertisements
Chapters
2: Data Handling
3: Square-Square Root and Cube-Cube Root
4: Linear Equation In One Variable
5: Understanding Quadrilaterals and Practical Geometry
6: Visualising Solid Shapes
7: Algebraic Expression, Identities and Factorisation
8: Exponents and Powers
9: Comparing Quantities
▶ 10: Direct and Inverse Proportions
11: Mensuration
12: Introduct To Graphs
13: Playing With Numbers
![NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 10 - Direct and Inverse Proportions NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 10 - Direct and Inverse Proportions - Shaalaa.com](/images/mathematics-english-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 10: Direct and Inverse Proportions
Below listed, you can find solutions for Chapter 10 of CBSE NCERT Exemplar for Mathematics [English] Class 8.
NCERT Exemplar solutions for Mathematics [English] Class 8 10 Direct and Inverse Proportions Exercise [Pages 315 - 330]
Choose the correct alternative:
Both u and v vary directly with each other. When u is 10, v is 15, which of the following is not a possible pair of corresponding values of u and v?
2 and 3
8 and 12
15 and 20
25 and 37.5
Both x and y vary inversely with each other. When x is 10, y is 6, which of the following is not a possible pair of corresponding values of x and y?
12 and 5
15 and 4
25 and 2.4
45 and 1.3
Assuming land to be uniformly fertile, the area of land and the yield on it vary ______
directly with each other.
inversely with each other.
neither directly nor inversely with each other.
sometimes directly and sometimes inversely with each other.
The number of teeth and the age of a person vary ______
directly with each other.
inversely with each other.
neither directly nor inversely with each other.
sometimes directly and sometimes inversely with each other.
A truck needs 54 litres of diesel for covering a distance of 297 km. The diesel required by the truck to cover a distance of 550 km is ______.
100 litres
50 litres
25.16 litres
25 litres
By travelling at a speed of 48 kilometres per hour, a car can finish a certain journey in 10 hours. To cover the same distance in 8 hours, the speed of the car should be ______.
60 km/h
80 km/h
30 km/h
40 km/h
In which of the following case, do the quantities vary directly with each other?
x 0.5 2 8 32 y 2 8 32 128 p 12 22 32 42 q 13 23 33 43 r 2 5 10 25 50 s 25 10 5 2 0.5 u 2 4 6 9 12 v 18 9 6 4 3
Which quantities in the previous question vary inversely with each other?
x and y
p and q
r and s
u and v
Which of the following vary inversely with each other?
Speed and distance covered.
Distance covered and taxi fare.
Distance travelled and time taken.
Speed and time taken.
Both x and y are in direct proportion, then `1/x` and `1/y` are ______
in indirect proportion.
in inverse proportion.
neither in direct nor in inverse proportion.
sometimes in direct and sometimes in inverse proportion.
Meenakshee cycles to her school at an average speed of 12 km/h and takes 20 minutes to reach her school. If she wants to reach her school in 12 minutes, her average speed should be ______.
`20/3` km/h
16 km/h
20 km/h
15 km/h
100 persons had food provision for 24 days. If 20 persons left the place, the provision will last for ______.
30 days
`96/5` days
120 days
40 days
If two quantities x and y vary directly with each other, then ______
`x/y` remains constant.
x – y remains constant.
x + y remains constant.
x × y remains constant.
If two quantities p and q vary inversely with each other, then ______
`p/q` remains constant.
p + q remains constant.
p × q remains constant.
p – q remains constant.
If the distance travelled by a rickshaw in one hour is 10 km, then the distance travelled by the same rickshaw with the same speed in one minute is ______.
`250/9` m
`500/9` m
1000 m
`500/3` m
Both x and y vary directly with each other and when x is 10, y is 14, which of the following is not a possible pair of corresponding values of x and y?
25 and 35
35 and 25
35 and 49
15 and 21
Fill in the blanks:
If x = 5y, then x and y vary ______ with each other.
If xy = 10, then x and y vary ______ with each other.
When two quantities x and y are in ______ proportion or vary ______ they are written as `x oo y`.
When two quantities x and y are in ______ proportion or vary ______ they are written as `x oo 1/y`.
Both x and y are said to vary ______ with each other if for some positive number k, xy = k.
x and y are said to vary directly with each other if for some positive number k, ______ = k.
Two quantities are said to vary ______ with each other if they increase (decrease) together in such a manner that the ratio of their corresponding values remains constant.
Two quantities are said to vary ______ with each other if an increase in one causes a decrease in the other in such a manner that the product of their corresponding values remains constant.
If 12 pumps can empty a reservoir in 20 hours, then time required by 45 such pumps to empty the same reservoir is ______ hours.
If x varies inversely as y, then
| x | – | 60 |
| y | 2 | 10 |
If x varies directly as y, then
| x | 12 | 6 |
| y | 48 | – |
When the speed remains constant, the distance travelled is ______ proportional to the time.
On increasing a, b increases in such a manner that `a/b` remains ______ and positive, then a and b are said to vary directly with each other.
If on increasing a, b decreases in such a manner that ______ remains ______ and positive, then a and b are said to vary inversely with each other.
If two quantities x and y vary directly with each other, then ______ of their corresponding values remains constant.
If two quantities p and q vary inversely with each other then ______ of their corresponding values remains constant.
The perimeter of a circle and its diameter vary ______ with each other.
A car is travelling 48 km in one hour. The distance travelled by the car in 12 minutes is ______.
An auto rickshaw takes 3 hours to cover a distance of 36 km. If its speed is increased by 4 km/h, the time taken by it to cover the same distance is ______.
If the thickness of a pile of 12 cardboard sheets is 45 mm, then the thickness of a pile of 240 sheets is ______ cm.
If x varies inversely as y and x = 4 when y = 6, then when x = 3 the value of y is ______.
In direct proportion, `a_1/b_1` ______ `a_2/b_2`
In case of inverse proportion, `a_2/- = b_2/-`
If the area occupied by 15 postal stamps is 60 cm2, then the area occupied by 120 such postal stamps will be ______.
If 45 persons can complete a work in 20 days, then the time taken by 75 persons will be ______ hours.
Devangi travels 50 m distance in 75 steps, then the distance travelled in 375 steps is ______ km.
State whether the following statement is True or False:
Two quantities x and y are said to vary directly with each other if for some rational number k, xy = k.
True
False
When the speed is kept fixed, time and distance vary inversely with each other.
True
False
When the distance is kept fixed, speed and time vary directly with each other.
True
False
Length of a side of a square and its area vary directly with each other.
True
False
Length of a side of an equilateral triangle and its perimeter vary inversely with each other.
True
False
If d varies directly as t2, then we can write dt2 = k, where k is some constant.
True
False
If a tree 24 m high casts a shadow of 15 m, then the height of a pole that casts a shadow of 6 m under similar conditions is 9.6 m.
True
False
If x and y are in direct proportion, then (x – 1) and (y – 1) are also in direct proportion.
True
False
If x and y are in inverse proportion, then (x + 1) and (y + 1) are also in inverse proportion.
True
False
If p and q are in inverse variation then (p + 2) and (q – 2) are also in inverse proportion.
True
False
If one angle of a triangle is kept fixed then the measure of the remaining two angles vary inversely with each other.
True
False
When two quantities are related in such a manner that, if one increases, the other also increases, then they always vary directly.
True
False
When two quantities are related in such a manner that if one increases and the other decreases, then they always vary inversely.
True
False
If x varies inversely as y and when x = 6, y = 8, then for x = 8 the value of y is 10.
True
False
The number of workers and the time to complete a job is a case of direct proportion.
True
False
For fixed time period and rate of interest, the simple interest is directly proportional to the principal.
True
False
The area of cultivated land and the crop harvested is a case of direct proportion.
True
False
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
The time taken by a train to cover a fixed distance and the speed of the train.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
The distance travelled by CNG bus and the amount of CNG used.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
The number of people working and the time to complete a given work.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
Income tax and the income.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
Distance travelled by an auto-rickshaw and time taken.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
Number of students in a hostel and consumption of food.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
Area of the walls of a room and the cost of white washing the walls.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
The number of people working and the quantity of work.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
Simple interest on a given sum and the rate of interest.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
Compound interest on a given sum and the sum invested.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
The quantity of rice and its cost.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
The height of a tree and the number of years.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
Increase in cost and number of shirts that can be purchased if the budget remains the same.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
Area of land and its cost.
Write whether the following statement vary directly, vary inversely with each other, or neither of the two.
Sales Tax and the amount of the bill.
Solve the following:
If x varies inversely as y and x = 20 when y = 600, find y when x = 400.
The variable x varies directly as y and x = 80 when y is 160. What is y when x is 64?
l varies directly as m and l is equal to 5, when `m = 2/3`. Find l when `m = 16/3`.
If x varies inversely as y and y = 60 when x = 1.5. Find x. when y = 4.5.
In a camp, there is enough flour for 300 persons for 42 days. How long will the flour last if 20 more persons join the camp?
A contractor undertook a contract to complete a part of a stadium in 9 months with a team of 560 persons. Later on, it was required to complete the job in 5 months. How many extra persons should he employ to complete the work?
Sobi types 108 words in 6 minutes. How many words would she type in half an hour?
A car covers a distance in 40 minutes with an average speed of 60 km/h. What should be the average speed to cover the same distance in 25 minutes?
It is given that l varies directly as m. Write an equation which relates l and m.
It is given that l varies directly as m. Find the constant of proportion (k), when l is 6 then m is 18.
It is given that l varies directly as m. Find l, when m is 33.
It is given that l varies directly as m. Find m when l is 8.
If a deposit of Rs 2,000 earns an interest of Rs 500 in 3 years, how much interest would a deposit of Rs 36,000 earn in 3 years with the same rate of simple interest?
The mass of an aluminum rod varies directly with its length. If a 16 cm long rod has a mass of 192 g, find the length of the rod whose mass is 105 g.
Find the values of x and y if a and b are in inverse proportion:
- 12 x 8
- 30 5 y
If Naresh walks 250 steps to cover a distance of 200 metres, find the distance travelled in 350 steps.
A car travels a distance of 225 km in 25 litres of petrol. How many litres of petrol will be required to cover a distance of 540 kilometres by this car?
From the following table, determine if x and y are in direct proportion or not.
| x | 3 | 6 | 15 | 20 | 30 |
| y | 12 | 24 | 45 | 60 | 120 |
From the following table, determine if x and y are in direct proportion or not.
| x | 4 | 7 | 10 | 16 |
| y | 24 | 42 | 60 | 96 |
From the following table, determine if x and y are in direct proportion or not.
| x | 1 | 4 | 9 | 20 |
| y | 1.5 | 6 | 13.5 | 30 |
If a and b vary inversely to other, then find the values of p, q, r ; x, y, z and l, m, n.
| a | 6 | 8 | q | 25 |
| b | 18 | p | 39 | r |
If a and b vary inversely to other, then find the values of p, q, r ; x, y, z and l, m, n.
| a | 2 | y | 6 | 10 |
| b | x | 12.5 | 15 | z |
If a and b vary inversely to other, then find the values of p, q, r ; x, y, z and l, m, n.
| a | l | 9 | n | 6 |
| b | 5 | m | 25 | 10 |
If 25 metres of cloth costs Rs 337.50, then what will be the cost of 40 metres of the same type of cloth?
If 25 metres of cloth costs Rs 337.50, then what will be the length of the cloth bought for Rs 810?
A swimming pool can be filled in 4 hours by 8 pumps of the same type. How many such pumps are required if the pool is to be filled in `2 2/3` hours?
The cost of 27 kg of iron is Rs 1,080, what will be the cost of 120 kg of iron of the same quality?
At a particular time, the length of the shadow of Qutub Minar whose height is 72 m is 80 m. What will be the height of an electric pole, the length of whose shadow at the same time is 1000 cm?
In a hostel of 50 girls, there are food provisions for 40 days. If 30 more girls join the hostel, how long will these provisions last?
Campus and Welfare Committee of school is planning to develop a blue shade for painting the entire school building. For this purpose various shades are tried by mixing containers of blue paint and white paint. In the following mixtures, decide which is a lighter shade of blue and also find the lightest blue shade among all of them.
| Mixture A | Mixture B |
 |
 |
If one container has one litre paint and the building requires 105 litres for painting, how many container of each type is required to paint the building by darkest blue shade?
Campus and Welfare Committee of school is planning to develop a blue shade for painting the entire school building. For this purpose various shades are tried by mixing containers of blue paint and white paint. In the following mixtures, decide which is a lighter shade of blue and also find the lightest blue shade among all of them.
| Mixture C | Mixture D |
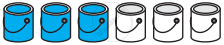 |
 |
If one container has one litre paint and the building requires 105 litres for painting, how many container of each type is required to paint the building by darkest blue shade?
Campus and Welfare Committee of school is planning to develop a blue shade for painting the entire school building. For this purpose various shades are tried by mixing containers of blue paint and white paint. In the following mixtures, decide which is a lighter shade of blue and also find the lightest blue shade among all of them.
| Mixture E | Mixture F |
 |
 |
If one container has one litre paint and the building requires 105 litres for painting, how many container of each type is required to paint the building by darkest blue shade?
Campus and Welfare Committee of school is planning to develop a blue shade for painting the entire school building. For this purpose various shades are tried by mixing containers of blue paint and white paint. In the following mixtures, decide which is a lighter shade of blue and also find the lightest blue shade among all of them.
| Mixture G | Mixture H |
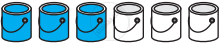 |
 |
If one container has one litre paint and the building requires 105 litres for painting, how many container of each type is required to paint the building by darkest blue shade?
Posing a question
Work with a partner to write at least five ratio statements about this quilt, which has white, blue, and purple squares.

How many squares of each colour will be there in 12 such quilts?
A packet of sweets was distributed among 10 children and each of them received 4 sweets. If it is distributed among 8 children, how many sweets will each child get?
44 cows can graze a field in 9 days. How many less/more cows will graze the same field in 12 days?
30 persons can reap a field in 17 days. How many more persons should be engaged to reap the same field in 10 days?
Shabnam takes 20 minutes to reach her school if she goes at a speed of 6 km/h. If she wants to reach school in 24 minutes, what should be her speed?
Ravi starts for his school at 8:20 a.m. on his bicycle. If he travels at a speed of 10 km/h, then he reaches his school late by 8 minutes but on travelling at 16 km/h he reaches the school 10 minutes early. At what time does the school start?
Match each of the entries in Column I with the appropriate entry in Column II
| Column I | Column II |
| 1. x and y vary inversely to each other | A. `x/y` = Constant |
| 2. Mathematical representation of inverse variation of quantities p and q |
B. y will increase in proportion |
| 3. Mathematical representation of direct variation of quantities m and n |
C. xy = Constant |
| 4. When x = 5, y = 2.5 and when y = 5, x = 10 | D. `p oo 1/q` |
| 5. When x = 10, y = 5 and when x = 20, y = 2.5 | E. y will decrease in proportion |
| 6. x and y vary directly with each other | F. x and y are directly proportional |
| 7. If x and y vary inversely then on decreasing x | G. `m oo n` |
| 8. If x and y vary directly then on decreasing x | H. x and y vary inversely |
| I. `p oo q` | |
| J. `m oo 1/n` |
There are 20 grams of protein in 75 grams of sauted fish. How many grams of protein is in 225 gm of that fish?
Ms. Anita has to drive from Jhareda to Ganwari. She measures a distance of 3.5 cm between these villages on the map. What is the actual distance between the villages if the map scale is 1 cm = 10 km?
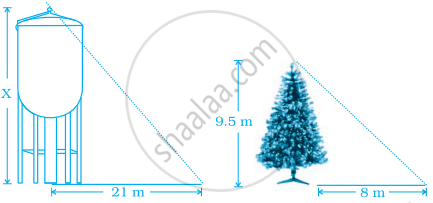
A water tank casts a shadow 21 m long. A tree of height 9.5 m casts a shadow 8 m long at the same time. The lengths of the shadows are directly proportional to their heights. Find the height of the tank.
The table shows the time four elevators take to travel various distances. Find which elevator is fastest and which is slowest.
| Distance (m) | Time (sec.) | |
| Elevator- A | 435 | 39 |
| Elevator- B | 448 | 28 |
| Elevator- C | 130 | 10 |
| Elevator- D | 85 | 5 |
How much distance will be travelled by elevators B and C separately in 140 sec? Who travelled more and by how much?
A volleyball court is in a rectangular shape and its dimensions are directly proportional to the dimensions of the swimming pool given below. Find the width of the pool.

A recipe for a particular type of muffins requires 1 cup of milk and 1.5 cups of chocolates. Riya has 7.5 cups of chocolates. If she is using the recipe as a guide, how many cups of milk will she need to prepare muffins?

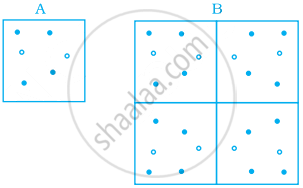
Pattern B consists of four tiles like pattern A. Write a proportion involving red dots and blue dots in pattern A and B. Are they in direct proportion? If yes, write the constant of proportion.
A bowler throws a cricket ball at a speed of 120 km/h. How long does this ball take to travel a distance of 20 metres to reach the batsman?
The variable x is inversely proportional to y. If x increases by p%, then by what percent will y decrease?
Here is a key board of a harmonium:
- Find the ratio of white keys to black keys on the keyboard.

- What is the ratio of black keys to all keys on the given keyboard.
- This pattern of keys is repeated on larger keyboard. How many black keys would you expect to find on a keyboard with 14 such patterns.
The following table shows the distance travelled by one of the new eco-friendly energy-efficient cars travelled on gas.
| Litres of gas | 1 | 0.5 | 2 | 2.5 | 3 | 5 |
| Distance (km) | 15 | 7.5 | 30 | 37.5 | 45 | 75 |
Which type of properties are indicated by the table? How much distance will be covered by the car in 8 litres of gas?
Kritika is following this recipe for bread. She realises her sister used most of sugar syrup for her breakfast. Kritika has only `1/6` cup of syrup, so she decides to make a small size of bread. How much of each ingredient shall she use?
Bread recipe
1 cup quick cooking oats
2 cups bread flour
`1/3` cup sugar syrup
1 tablespoon cooking oil
`1 1/3` cups water
3 tablespoons yeast
1 teaspoon salt.
Many schools have a recommended students-teacher ratio as 35:1. Next year, school expects an increase in enrolment by 280 students. How many new teachers will they have to appoint to maintain the students-teacher ratio?
Kusum always forgets how to convert miles to kilometres and back again. However she remembers that her car’s speedometer shows both miles and kilometres. She knows that travelling 50 miles per hour is same as travelling 80 kilometres per hour. To cover a distance of 200 km, how many miles Kusum would have to go?
The students of Anju’s class sold posters to raise money. Anju wanted to create a ratio for finding the amount of money her class would make for different numbers of posters sold. She knew they could raise Rs 250 for every 60 posters sold.
- How much money would Anju’s class make for selling 102 posters?
- Could Anju’s class raise exactly Rs 2,000? If so, how many posters would they need to sell? If not, why?
Solutions for 10: Direct and Inverse Proportions
![NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 10 - Direct and Inverse Proportions NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 10 - Direct and Inverse Proportions - Shaalaa.com](/images/mathematics-english-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 8 chapter 10 - Direct and Inverse Proportions
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 8 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 8 CBSE 10 (Direct and Inverse Proportions) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 8 chapter 10 Direct and Inverse Proportions are Concept of Direct Proportion, Concept of Inverse Proportion.
Using NCERT Exemplar Mathematics [English] Class 8 solutions Direct and Inverse Proportions exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 8 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 10, Direct and Inverse Proportions Mathematics [English] Class 8 additional questions for Mathematics Mathematics [English] Class 8 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
