Advertisements
Advertisements
Question
It is given that l varies directly as m. Find m when l is 8.
Solution
Since, l varies directly as m.
If `l = 8`
∴ `l/m = k`
⇒ `8/m = 1/3` ...`[∵ k = 1/3]`
⇒ m = 8 × 3 = 24
APPEARS IN
RELATED QUESTIONS
Suppose 2 kg of sugar contains 9 × 106 crystals.
How many sugar crystals are there in
- 5 kg of sugar?
- 1.2 kg of sugar?
A and B can do a piece of work in 12 days; B and C in 15 days; C and A in 20 days. How much time will A alone take to finish the work?
The cost of 12 quintals of soyabean is 36,000 rupees. How much will 8 quintals cost?
Distance travelled by a bus and time taken are in direct proportion
Meenakshee cycles to her school at an average speed of 12 km/h and takes 20 minutes to reach her school. If she wants to reach her school in 12 minutes, her average speed should be ______.
Both x and y vary directly with each other and when x is 10, y is 14, which of the following is not a possible pair of corresponding values of x and y?
On increasing a, b increases in such a manner that `a/b` remains ______ and positive, then a and b are said to vary directly with each other.
It is given that l varies directly as m. Find the constant of proportion (k), when l is 6 then m is 18.
Match each of the entries in Column I with the appropriate entry in Column II
| Column I | Column II |
| 1. x and y vary inversely to each other | A. `x/y` = Constant |
| 2. Mathematical representation of inverse variation of quantities p and q |
B. y will increase in proportion |
| 3. Mathematical representation of direct variation of quantities m and n |
C. xy = Constant |
| 4. When x = 5, y = 2.5 and when y = 5, x = 10 | D. `p oo 1/q` |
| 5. When x = 10, y = 5 and when x = 20, y = 2.5 | E. y will decrease in proportion |
| 6. x and y vary directly with each other | F. x and y are directly proportional |
| 7. If x and y vary inversely then on decreasing x | G. `m oo n` |
| 8. If x and y vary directly then on decreasing x | H. x and y vary inversely |
| I. `p oo q` | |
| J. `m oo 1/n` |
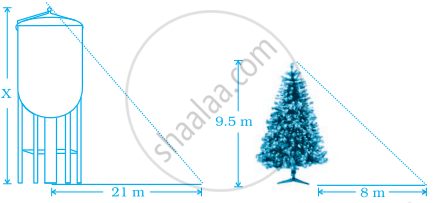
A water tank casts a shadow 21 m long. A tree of height 9.5 m casts a shadow 8 m long at the same time. The lengths of the shadows are directly proportional to their heights. Find the height of the tank.