Advertisements
Advertisements
Question
The product of two negative terms is a negative term.
Options
True
False
Solution
This statement is False.
Explanation:
Since, the product of two negative terms is always a positive term, i.e. (–) × (–) = (+).
APPEARS IN
RELATED QUESTIONS
State whether a given pair of term is of like or unlike term.
14xy, 42yx
State whether a given pair of term is of like or unlike term.
4m2p, 4mp2
State whether a given pair of term is of like or unlike term.
12xz, 12x2z2
Simplify the following:
\[\frac{11}{2} x^2 y - \frac{9}{4}x y^2 + \frac{1}{4}xy - \frac{1}{14} y^2 x + \frac{1}{15}y x^2 + \frac{1}{2}xy\]
Simplify the following:
\[\left( \frac{1}{3} y^2 - \frac{4}{7}y + 11 \right) - \left( \frac{1}{7}y - 3 + 2 y^2 \right) - \left( \frac{2}{7}y - \frac{2}{3} y^2 + 2 \right)\]
Simplify the following: \[- \frac{1}{2} a^2 b^2 c + \frac{1}{3}a b^2 c - \frac{1}{4}ab c^2 - \frac{1}{5}c b^2 a^2 + \frac{1}{6}c b^2 a - \frac{1}{7} c^2 ab + \frac{1}{8}c a^2 b .\]
In the polynomial, given below, separate the like terms :
y2z3, xy2z3, −5x2yz, −4y2z3, −8xz3y2, 3x2yz and 2z3y2
Find the product of the terms
3x2y , −3xy3, x2y2
Identify the like terms among the following:
7x, 5y, −8x, 12y, 6z, z, −12x, −9y, 11z
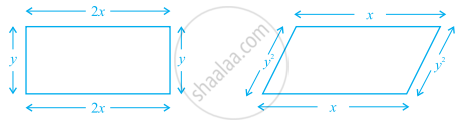
The unlike terms in perimeters of following figures are ______ and ______.