Advertisements
Advertisements
प्रश्न
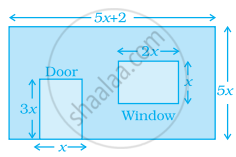
The figure shows the dimensions of a wall having a window and a door of a room. Write an algebraic expression for the area of the wall to be painted.
Advertisements
उत्तर
We have a wall of dimension 5x × (5x + 2) having a window and a door of dimension (2x × x) and (3x × x), respectively.
Then, area of the window = 2x × x = 2x2 sq.units
Area of the door = 3x × x = 3x2 sq.units
And area of wall = (5x + 2) × 5x = (25x2 + 10x) sq.units
Now, area of the required part of the wall to be painted
= Area of the wall – (Area of the window + Area of the door)
= 25x2 + 10x – (2x2 + 3x2)
= 25x2 + 10x – 5x2
= 20x2 + 10x
= 2 × 2 × 5 × x × x + 2 × 5 × x
= 2 × 5 × x(2x + 1)
= 10x(2x + 1) sq.units
APPEARS IN
संबंधित प्रश्न
Factorize x3 - 2x2 y + 3xy2 - 6y3
Factorize 4( x - y)2 -12( x - y)( x + y ) + 9(x + y )2
(2x - 3y)3 + (4z - 2x)3 + (3y - 4z )3
Find the value of the following expression: 64x2 + 81y2 + 144xy, when x = 11 and \[y = \frac{4}{3}\]
The expression x4 + 4 can be factorized as
Evaluate:
(i) (a + b)(a - b)
(ii) (a2 + b2)(a + b)(a - b); using the result of (i).
(iii) (a4 + b4)(a2 + b2)(a + b)(a - b); using the result of (ii).
Divide: 4x3 - 2x2 by - x
Divide: x2 + 4xy + 4y2 by x + 2y
The solution of the equation `"3x" - 1/2 = 5/2 + "x"` is ______.
A school has a rectangular playground with length x and breadth y and a square lawn with side x as shown in the figure given below. What is the total perimeter of both of them combined together?
