Advertisements
Advertisements
प्रश्न
There is a number in the box `square` such that `square`, 24, 9, 12 are in proportion. The number in the box is ______.
उत्तर
There is a number in the box `square` such that `square`, 24, 9, 12 are in proportion. The number in the box is 18.
Explanation:
Let the number in box is x, then x, 24, 9 and 12 are in proportion.
∴ x : 24 :: 9 : 12
⇒ `x/24 = 9/12` .....[∵ If a, b, c and d are in proportion, then `a/b = c/d`]
⇒ `x xx 12 = 24 xx 9` .....[By cross-multiplication]
⇒ `x = (24 xx 9)/12`
⇒ `x = 2 xx 9`
∴ x = 18
The number in the box is 18.
APPEARS IN
संबंधित प्रश्न
If a, b and c are in continued proportion, prove that `(a^2 + b^2 + c^2)/(a + b + c)^2 = (a - b + c)/(a + b + c)`
Check whether the following numbers are in continued proportion.
1, 2, 3
Check whether the following numbers are in continued proportion.
3, 5, 8
If u, v, w, and x are in continued proportion, then prove that (2u+3x) : (3u+4x) : : (2u3+3v3) : (3u3+4v3)
If ax = by = cz, prove that
`x^2/(yz) + y^2/(zx) + z^2/(xy) = (bc)/a^2 + (ca)/b^2 + (ab)/c^2`.
If a, b, c, d are in continued proportion, prove that (b - c)2 + (c - a)2 + (d - b)2 = (d - a)2.
Find the fourth proportional to `(1)/(3), (1)/(4), (1)/(5)`
Find the third proportional to 0.24, 0.6
Write (T) for true and (F) for false in case of the following:
30 bags : 18 bags : : Rs 450 : Rs 270
Unequal masses will not balance on a fulcrum if they are at equal distance from it; one side will go up and the other side will go down.
Unequal masses will balance when the following proportion is true:
`("mass"1)/("length"2) = ("mass"2)/("length"1)`
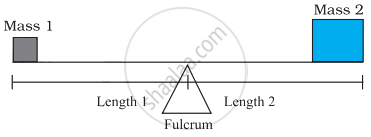
Two children can be balanced on a seesaw when
`("mass"1)/("length"2) = ("mass"2)/("length"1)`. The child on the left and child on the right are balanced. What is the mass of the child on the right?