Advertisements
Advertisements
प्रश्न
Three different coins are tossed together. Find the probability of getting at least two heads.
उत्तर
When three coins are tossed together, the possible outcomes are
HHH, HTH, HHT, THH, THT, TTH, HTT, TTT
∴ Total number of possible outcomes = 8
Favourable outcomes of at least two heads are HHH, HTH, HHT, THH
∴ Total number of favourable outcomes = 4
∴ P(at least two heads) =`4/8=1/2`
संबंधित प्रश्न
In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be double of the class in which they are studying. If there are 1to 12 classes in the school and each class has two sections, find how many trees were
planted by the students. Which value is shown in this question?
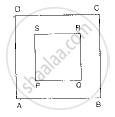
In the given figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square?
Two different dice are rolled simultaneously. Find the probability that the sum of numbers appearing on the two dice is 10 ?
In a class of 42 students in Model High School, 3 students use spectacles.
Fill in the following boxes to find the probability of a students selected
at random is wearing sepctacles.
The total number of students in the class is 42.
∴n(S) = ...... ,
Let the event, a student uses spectacles, be A.
∴ n(A) = ...........
∴ P(A) = ............ ∴ P(A) = ............
Two coins are tossed simultaneously. Find the probability of getting exactly one head.
Which of the following cannot be the probability of an event?
A bag contains 4 white balls, 5 red balls, 2 black balls and 4 green balls. A ball is drawn at random from the bag. Find the probability that it is black.
A bag contains 4 white balls, 5 red balls, 2 black balls and 4 green balls. A ball is drawn at random from the bag. Find the probability that it is red or white.
A lot consists of 144 ballpoint pens of which 20 are defective and others good. Tanvy will buy a pen if it is good, but will not buy it if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that she will buy it,
A game consists of tossing a coin 3 times and noting the outcome each time. If getting the same result in all the tosses is a success, find the probability of losing the game.
In a single throw of a die, find the probability of getting a number
(i) greater than 2
(ii) less than or equal to 2
(iii) not greater than 2.
In a single throw of a die, find the probability that the number:
(i) will be an even number.
(ii) will be an odd number.
(iii) will not be an even number.
Two coins are tossed together. What is the probability of getting:
(i) at least one head
(ii) both heads or both tails.
A coin is tossed once. Find the probability of not getting a head
You are walking along a street. If you just choose a stranger crossing you, what is the probability that his next birthday will fall on a Sunday?
Frame two problems in calculating probability, based on the spinner shown here.
The probability that a non leap year selected at random will contain 53 sundays is ______.
A coin is tossed 12 times and the outcomes are observed as shown below:
The chance of occurrence of Head is
A dice is rolled once. What is the probability that the number on top will be odd
A bag contains 25 cards, numbered through 1 to 25. A card is drawn at random. What is the probability that the number on the card drawn is a prime number?
