Advertisements
Advertisements
प्रश्न
Three equal cubes are placed adjacently in a row. Find the ratio of total surface area of the new cuboid to that of the sum of the surface areas of the three cubes.
उत्तर
\[\text { Suppose that the side of the cube }= x cm\]
\[\text { Surface area of the cube = 6 }\times \text { (side })^2 = 6 \times x^2 = 6 x^2 {cm}^2 \]
\[\text { i . e . , the sum of the surface areas of three such cubes }= 6 x^2 + 6 x^2 + 6 x^2 = 18 x^2 {cm}^2 \]
\[\text { Now, these three cubes area placed together to form a cuboid . } \]
\[\text { Then the length of the new cuboid will be 3 times the edge of the cube } = 3 \times x = 3x cm\]
\[\text { Breadth of the cuboid = x cm }\]
\[\text { Height of the cuboid = x cm }\]
\[ \therefore\text { Total surface area of the cuboid = 2 } \times\text { (length }\times\text { breadth + breadth }\times\text { height + length } \times\text { height) }\]
\[ = 2 \times (3x \times x + x \times x + 3x \times x)\]
\[ = 2 \times (3 x^2 + x^2 + 3 x^2 )\]
\[ = 2 \times (7 x^2 )\]
\[ = 14 x^2 cm\]
2
i.e., the ratio of the total surface area cuboid to the sum of the surface areas of the three cubes =
\[14 x^2 c m^2 : 18 x^2 c m^2 \]
\[ = 7: 9\]
APPEARS IN
संबंधित प्रश्न
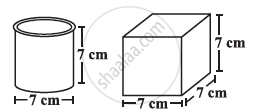
Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
Find the volume of a cube whose side is 4 cm .
Suppose that there are two cubes, having edges 2 cm and 4 cm, respectively. Find the volumes V1and V2 of the cubes and compare them.
Find the volume in cubic decimetre of the cube whose side is 2 dm 5 cm .
Fill in the blank in the following so as to make the statement true:
1 litre = ....... cubic decimetre
Fill in the blank in the following so as to make the statement true:
1 litre = ........ cu. cm
Find the volume of a cube whose surface area is 150 m2 .
Find the cost of sinking a tubewell 280 m deep, having diameter 3 m at the rate of Rs 3.60 per cubic metre. Find also the cost of cementing its inner curved surface at Rs 2.50 per square metre.
The edges of three cubes of metal are 3 cm, 4 cm, and 5 cm. They are melted and formed into a single cube. Find the edge of the new cube.
Three equal cubes are placed adjacently in a row. Find the ratio of the total surfaced area of the resulting cuboid to that of the sum of the total surface areas of the three cubes.
