Advertisements
Advertisements
प्रश्न
"त्रिकोणाच्या एका बाजूला समांतर असणारी रेषा त्याच्या उरलेल्या बाजूंना भिन्न बिंदूत छेदत असेल, तर ती रेषा त्या बाजूंना एकाच प्रमाणात विभागते.” हे सिद्ध करा.
उत्तर
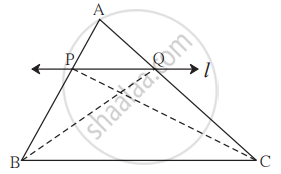
पक्ष: ΔABC मध्ये रेषा l || रेख BC आणि रेषा l ही बाजू AB ला P मध्ये व बाजू AC ला Q मध्ये छेदते.
साध्य: `"AP"/"PB" = "AQ"/"QC"`
रचना: रेख PC व रेख BQ काढा.
सिद्धता: ΔAPQ आणि ΔBPQ यांचा Q हा सामाईक शिरोबिंदू आहे आणि त्यांचे AP व BP हे पाया AB या एकाच रेषेवर आहेत. त्यामुळे हे समान उंचीचे त्रिकोण आहेत.
`therefore ("A"(Delta "APQ"))/("A"(Delta "BPQ")) = "AP"/"PB"` ...(i) [समान उंचीचे त्रिकोण]
तसेच, ΔAPQ आणि ΔCPQ यांचा P हा सामाईक शिरोबिंदू आहे आणि त्यांचे AQ व QC हे पाया AC या एकाच रेषेवर आहेत. त्यामुळे हे समान उंचीचे त्रिकोण आहेत.
∴ `("A"(Delta "APQ"))/("A"(Delta "CPQ")) = "AQ"/"QC"` ...(ii) [समान उंचीचे त्रिकोण]
ΔBPQ व ΔCPQ यांचा रेख PQ हा समान पाया आहे.
ΔBPQ आणि ΔCPQ हे PQ व BC ह्या दोन समांतर रेषांमध्ये बद्ध आहेत.
∴ ΔBPQ व ΔCPQ ची उंची समान आहे.
∴ A(ΔBPQ) = A(ΔCPQ) ...(iii) [समान उंची व समान पाया असलेल्या त्रिकोणांची क्षेत्रफळे समान असतात.]
∴`("A"(Delta "APQ"))/("A"(Delta "BPQ")) = ("A"(Delta "APQ"))/("A"(Delta "CPQ"))` ...(iv) [(i), (ii) आणि (iii) वरून]
∴ `"AP"/"PB" = "AQ"/"QC"` ...[(i), (ii) व (iv) वरून]
APPEARS IN
संबंधित प्रश्न
जर Δ PQR मध्ये PM = 15, PQ = 25, PR = 20, NR = 8 तर रेषा NM ही बाजू RQ ला समांतर आहे का? कारण लिहा.
आकृतीत काही कोनांची मापे दिली आहेत त्यावरून दाखवा, की `"AP"/"PB"= "AQ"/"QC"`
दिलेल्या आकृती मध्ये त्रिकोणाच्या अंतर्भागात X हा एक कोणताही बिंदू आहे. बिंदू X हा त्रिकोणाच्या शिरोबिंदूंशी जोडला आहे. तसेच रेख PQ || रेख DE, रेख QR || रेख EF तर रेख PR || रेख DF हे सिद्ध करण्यासाठी खालील चौकटी पूर्ण करा.
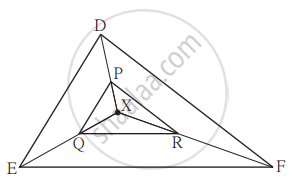
सिद्धता: Δ XDE मध्ये PQ || DE .............. `square`
∴ `"XP"/square = square/"QE"` ...........(I) (प्रमाणाचे मूलभूत प्रमेय )
Δ XEF मध्ये QR || EF ................. `square`
∴ `square/square` = `square/square` ..........(II) `square`
∴ `square/square` = `square/square` .......... विधान (I) व (II) वरून
∴ रेख PR || रेख DF .......... (प्रमाणाच्या मूलभूत प्रमेयाचा व्यत्यास)
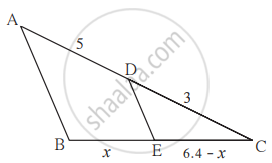
आकृती मध्ये A – D – C व B – E – C . रेख DE || बाजू AB. जर AD = 5, DC = 3, BC = 6.4 तर BE काढा.
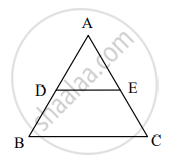
आकृतीमध्ये रेख DE || रेख BC, तर पुढीलपैकी सत्य विधान कोणते?
आकृतीमध्ये रेषा BC || रेषा DE, AB = 2, BD = 3, AC = 4 व CX = x तर x ची किंमत काढा.

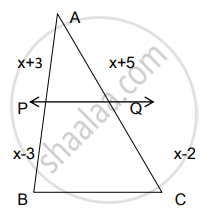
आकृतीमध्ये रेख PQ || बाजू BC, AP = x + 3, PB = x - 3, AQ = x + 5, QC = x – 2, तर x ची किंमत काढण्यासाठी पुढील कृती पूर्ण करा.
∆PQB मध्ये रेख PQ || बाजू BC.
`"AP"/"PB" = "AQ"/square` ...........[`square`]
`(x + 3)/(x - 3) = (x + 5)/square`
(x + 3) `square` = (x + 5) (x– 3)
x2 + x – `square` = x2 + 2x – 15
x = `square`
आकृतीमध्ये, PS = 2, SQ = 6, QR = 5, PT = x आणि TR = y, तर x व y च्या योग्य किमतीच्या अशा जोड्या शोधा, की ज्यामुळे रेषा ST || बाजू QR असेल.