Advertisements
Advertisements
प्रश्न
Two bodies A and B whose masses are in the ratio 1 : 2 are suspended from two separate massless springs of force constants kA and kB respectively. If the two bodies oscillate vertically such that their maximum velocities are in the ratio 1 : 2, the ratio of the amplitude A to that of B is
विकल्प
`sqrt(("k"_"B")/(2"k"_"A"))`
`sqrt(("k"_"B")/(8"k"_"A"))`
`sqrt((2"k"_"B")/("k"_"A"))`
`sqrt((8"k"_"B")/("k"_"A"))`
उत्तर
`sqrt(("k"_"B")/(8"k"_"A"))`
APPEARS IN
संबंधित प्रश्न
A spring is connected to a mass m suspended from it and its time period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is
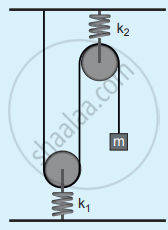
The time period for small vertical oscillations of block of mass m when the masses of the pulleys are negligible and spring constant k1 and k2 is
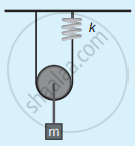
An ideal spring of spring constant k, is suspended from the ceiling of a room and a block of mass M is fastened to its lower end. If the block is released when the spring is un-stretched, then the maximum extension in the spring is
A pendulum is hung in a very high building oscillates to and fro motion freely like a simple harmonic oscillator. If the acceleration of the bob is 16 ms−2 at a distance of 4 m from the mean position, then the time period is
Write down the equation of the time period for the linear harmonic oscillator.
Discuss the simple pendulum in detail.
Explain the horizontal oscillations of a spring.
Describe the vertical oscillations of a spring.
A piece of wood of mass m is floating erect in a liquid whose density is ρ. If it is slightly pressed down and released, then executes simple harmonic motion. Show that its time period of oscillation is T = `2π sqrt("m"/("Ag"ρ))`
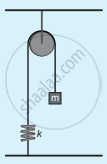
Compute the time period for the following system if the block of mass m is slightly displaced vertically down from its equilibrium position and then released. Assume that the pulley is light and smooth, strings and springs are light.