Advertisements
Advertisements
प्रश्न
Two circles intersect each other at points A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
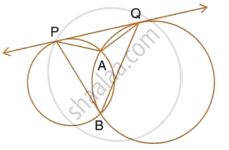
उत्तर
Join AB.
PQ is the tangent and AB is a chord
∴ ∠QPA = ∠PBA ...(i) (Angles in alternate segment)
Similarly,
∠PQA = ∠QBA ...(ii)
Adding (i) and (ii)
∠QPA + ∠PQA = ∠PBA + ∠QBA
But, in ΔPAQ,
∠QPA + ∠PQA = 180° – ∠PAQ ...(iii)
And ∠PBA + ∠QBA = ∠PBQ ...(iv)
From (iii) and (iv)
∠PBQ = 180° – ∠PAQ
`=>` ∠PBQ + ∠PAQ = 180°
`=>` ∠PBQ + ∠PBQ = 180°
Hence ∠PAQ and ∠PBQ are supplementary.
APPEARS IN
संबंधित प्रश्न
Two circles of radii 5 cm and 3 cm are concentric. Calculate the length of a chord of the outer circle which touches the inner.
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centres if:
- they touch each other externally,
- they touch each other internally.
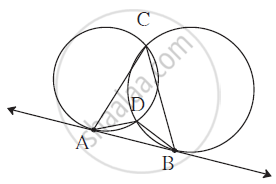
In the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:

(ii) angles APB = 90°
Two parallel tangents of a circle meet a third tangent at points P and Q. Prove that PQ subtends a right angle at the centre.
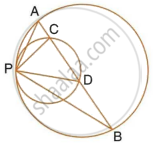
Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that ∠CPA = ∠DPB.
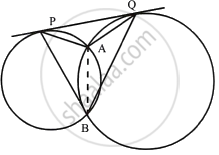
Two circles intersect each other at points C and D. Their common tangent AB touches the circles at point A and B. Prove that :
∠ ADB + ∠ ACB = 180°
Two circles of radii 5cm and 3cm with centres O and P touch each other internally. If the perpendicular bisector of the line segment OP meets the circumference of the larger circle at A and B, find the length of AB.
Radii of two circles are 6.3 cm and 3.6 cm. State the distance between their centers if -
they touch each other internally.
P and Q are the centre of circles of radius 9 cm and 2 cm respectively; PQ = 17 cm. R is the centre of circle of radius x cm, which touches the above circles externally, given that ∠ PRQ = 90°. Write an equation in x and solve it.
Two circles with centres O and O' touch each other at point L. Prove that, a tangent through L bisects the common tangent AB of the two circles at point M.
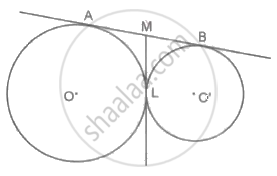
Given: AB is a common tangent of the two circles that touch each other at point L. ML is a tangent through point L.
To prove: M is a mid-point of the tangent AB or MA = MB.
Proof: From the figure,
M is an external point that draws two tangents, MA and ML to the circle with the centre O.
So, `square` = `square` ......(i)
Similarly, M draws two tangents ML and MB to the circle with the centre O'.
So, `square` = `square` ......(ii)
From the equations (i) and (ii),
`square` = `square`
Hence, the tangent at the point L, bisects the common tangent, AB of the two circles at point M.
