Advertisements
Advertisements
प्रश्न
Two coherent sources of different intensities send waves which interfere. The ratio of maximum intensity to the minimum intensity is 25. The intensities of the sources are in the ratio ______.
विकल्प
25 : 1
5 : 1
9 : 4
625 : 1
उत्तर
Two coherent sources of different intensities send waves which interfere. The ratio of maximum intensity to minimum intensity is 25. The intensities of the sources are in the ratio 9 : 4.
Explanation:
The ratio of maximum intensity and minimum intensity is given by,
`I_(max) = (sqrtI_1 + sqrtI_2)^2, I_(min) = (sqrtI_1 - sqrtI_2)^2`
∴ `I_(max)/I_(min) = ((sqrtI_1 + sqrtI_2)/(sqrtI_1 - sqrtI_2))^2 = 25`
`(sqrtI_1 + sqrtI_2)/(sqrtI_1 - sqrtI_2) = 5`
⇒ `(sqrt(I_1/I_2) + 1)/(sqrt(I_1/I_2)- 1) = 5`
⇒ `sqrt(I_1/I_2) + 1 = 5sqrt(I_1/I_2) - 5`
⇒ `6 = 4sqrt(I_1/I_2)`
⇒ `sqrt(I_1/I_2) = 3/2`
⇒ `I_1/I_2 = 9/4`
APPEARS IN
संबंधित प्रश्न
When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why?
Two sources are called coherent if they produce waves ______________ .
Two coherent point sources S1 and S2, vibrating in phase, emit light of wavelength \[\lambda.\] The separation between the sources is \[2\lambda.\] Consider a line passing through S2 and perpendicular to the line S1 S2. What is the smallest distance from S2 where a minimum intensity occurs?
Two sources of light are coherent if they have ______.
Two source S1 and S2 of intensity I1 and I2 are placed in front of a screen [Figure (a)]. The pattern of intensity distribution seen in the central portion is given by Figure (b).
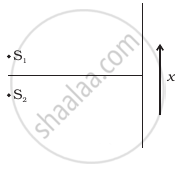 (a) |
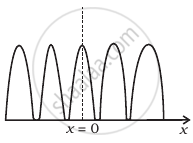 (b) |
- S1 and S2 have the same intensities.
- S1 and S2 have a constant phase difference.
- S1 and S2 have the same phase.
- S1 and S2 have the same wavelength.
n identical waves each of intensity I0 interfere with each other. The ratio of maximum intensities if the interference is (i) coherent and (ii) incoherent is ______.
