Advertisements
Advertisements
प्रश्न
When a drop of oil is spread on a water surface, it displays beautiful colours in daylight because of ______________ .
विकल्प
disperson of light
reflection of light
polarization of light
interference of light
उत्तर
interference of light
Interference effect is produced by a thin film ( coating of a thin layer of a translucent material on a medium of different refractive index which allows light to pass through it))In the present case, oil floating on water forms a thin film on the surface of water, leading to the display of beautiful colours in daylight because of the interference of sunlight.
APPEARS IN
संबंधित प्रश्न
State any one difference between interference of light and diffraction of light
Four light waves are represented by
(i) \[y = a_1 \sin \omega t\]
(ii) \[y = a_2 \sin \left( \omega t + \epsilon \right)\]
(iii) \[y = a_1 \sin 2\omega t\]
(iv) \[y = a_2 \sin 2\left( \omega t + \epsilon \right).\]
Interference fringes may be observed due to superposition of
(a) (i) and (ii)
(b) (i) and (iii)
(c) (ii) and (iv)
(d) (iii) and (iv)
Answer the following question.
Describe any two characteristic features which distinguish between interference and diffraction phenomena. Derive the expression for the intensity at a point of the interference pattern in Young's double-slit experiment.
Answer in brief:
What is meant by coherent sources?
What are the conditions for obtaining a good interference pattern? Give reasons.
The intensity of the light coming from one of the slits in Young's experiment is twice the intensity of the light coming from the other slit. What will be the approximate ratio of the intensities of the bright and dark fringes in the resulting interference pattern?
Two coherent sources whose intensity ratio is 25:1 produce interference fringes. Calculate the ratio of amplitudes of light waves coming from them.
Why two light sources must be of equal intensity to obtain a well-defined interference pattern?
Describe geometry of the Young’s double slit experiment with the help of a ray diagram. What is fringe width? Obtain an expression of it. Write the conditions for constructive as well as destructive interference.
Obtain the equation for bandwidth in Young’s double slit experiment.
A graph is plotted between the fringe-width Z and the distance D between the slit and eye-piece, keeping other adjustment same. The correct graph is
A.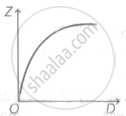 |
B. |
C.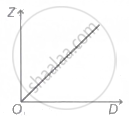 |
D.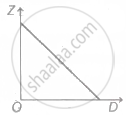 |
If the monochromatic source in Young's double slit experiment is white light, then ____________.
A thin transparent sheet is placed in front of a slit in Young's double slit experiment. The fringe width will ____________.
In Young's double-slit experiment, an interference pattern is obtained on a screen by a light of wavelength 4000 Å, coming from the coherent sources S1 and S2 At certain point P on the screen, third dark fringe is formed. Then the path difference S1P - S2P in microns is ______.
In interference experiment, intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at (sin30° = cos60° = 0.5, `lambda` = wavelength of light, d = slit width) ____________.
The graph shows the variation of fringe width (β) versus distance of the screen from the plane of the slits (D) in Young's double-slit experiment Keeping other parameters the same. The wavelength of light used can be calculated as d = distance between the slits ______

A double slit experiment is immersed in water of refractive index 1.33. The slit separation is 1 mm, distance between slit and screen is 1.33 m. The slits are illuminated by a light of wavelength 6300 Å. The fringe width is ______.
In an interference experiment, the intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at ____________.
(cos 60° = 0.5, `lambda` = wavelength of light, d = slit width)
If we have two coherent sources S1 and S2 vibrating in phase, then for an arbitrary point P constructive interference is observed whenever the path difference is ______.
In a double-slit experiment, the optical path difference between the waves coming from two coherent sources at a point P on one side of the central bright is 7.5 µm and that at a point Q on the other side of the central bright fringe and 1.8 µm. How many bright and dark fringes are observed between points P and Q if the wavelength of light used is 600 nm?
