Advertisements
Advertisements
प्रश्न
Describe geometry of the Young’s double slit experiment with the help of a ray diagram. What is fringe width? Obtain an expression of it. Write the conditions for constructive as well as destructive interference.
उत्तर
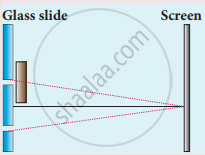
i. Let S1 and S2 be the two coherent monochromatic sources that are separated by short distance d. They emit light waves of wavelength λ.
ii. Let D = horizontal distance between screen and source.
iii. Draw S1M and S2N ⊥ AB
OP = perpendicular bisector of the slit.
Since S1P = S2P, the path difference between waves reaching P from S1 and S2 is zero, therefore there is a bright point at P.
iv. Consider a point Q on the screen which is at a distance y from the central point P on the screen. Light waves from S1 and S2 reach at Q simultaneously by covering paths S1Q and S2Q, where they superimpose. 
Derivation:
In Δ S1MQ, (S1Q)2 = (S1M)2 + (MQ)2
`("S"_1"Q")^2 = "D"^2 + ["y" - "d"/2]^2` ....(1)
In `Δ "S"_2"NQ", ("S"_2"Q")^2 = ("S"_2"N")^2 + ("NQ")^2`
∴ `("S"_2"Q")^2 = "D"^2 + ["y" + "d"/2]^2` ....(2)
Subtract equation (1) from (2),
`("S"_2"Q")^2 - ("S"_1"Q")^2 = ["D"^2 + ("y" + "d"/2)^2] - ["D"^2 + ("y" - "d"/2)^2]`
= `"D"^2 + ("y" + "d"/2)^2 - "D"^2 - ("y" - "d"/2)^2`
= `("y" + "d"/2)^2 - ("y" - "d"/2)^2`
= `("y"^2 + "d"^2/4 + "yd") - ("y"^2 + "d"^2/4 - "yd")`
= `"y"^2 + "d"^2/4 + "yd" - "y"^2 - "d"^2/4 + "yd"("S"_2"Q")^2 - ("S"_1"Q")^2`
= 2yd
∴ `("S"_2"Q" + "S"_1"Q")("S"_2"Q" - "S"_1"Q")` = 2yd
∴ `"S"_2"Q" - "S"_1"Q" = (2"yd")/("S"_2"Q" + "S"_1"Q")` ....(3)
If y << D and d << D then, S1Q ≈ S2Q ≈ D
S2Q + S1Q = 2D
∴ Equation (3) becomes,
`"S"_2"Q" - "S"_1"Q" = (2"yd")/(2"D")`
∴ `"S"_2"Q" - "S"_1"Q" = "yd"/"D"`
∴ Δl = `"yd"/"D"` ....(4)
Equation (4) gives the path difference of two interfering light waves. Point Q will be bright if,
Δl = nλ = 2n`lambda/2`
where n = 0, 1, 2,….
∴ `("y"_"n""d")/"D" = "n"λ = 2"n"lambda/2` ........….[From equation (4)]
∴ `"y"_"n" = "n"(lambda"D")/"d"` ….(5)
Equation (5) represents the distance of the nth bright fringe from the central bright fringe.
Point Q will be a dark point if,
`Deltal = (2"n" - 1)lambda/2`
where n = 1, 2, 3,……
∴ `("y"_"n"^'"d")/"D" = (2"n" - 1)lambda/2`
∴ `"y"_"n"^' = (2"n" - 1)(lambda"D")/(2"d") = ("n" - 1/2) (lambda"D")/"d"` .........(6)
Equation (6) represents the distance of nth dark fringe from the central maximum.
Fringe width:
The distance between any two successive dark or any two successive bright fringes is equal. This is called the fringe width and is given by, Fringe width = W = Δy = `"y"_("n" + 1) - "y"_"n" = "y"_"n + 1"^' - "y"_"n"^'`
W = `λ"D"/"d"`
Thus, both dark and bright fringes are equidistant and have equal widths.
Conditions for constructive and destructive interference:
The phase difference between the two waves reaching P, from `"S"_1` and `"S"_2` is given by,
`Deltaphi = "y""d"/"D"((2pi)/lambda)` ..........`(∵ Deltal = "yd"/"D")`
The condition for constructive interference in terms of phase difference is given by,
ΔΦ = n2π, where, n = 0, ±1 ±2
∴ The condition for destructive interference in terms of phase difference is given by
`Deltaphi = ("n" - 1/2)2pi,` where, n = ±1, ±2
APPEARS IN
संबंधित प्रश्न
Four light waves are represented by
(i) \[y = a_1 \sin \omega t\]
(ii) \[y = a_2 \sin \left( \omega t + \epsilon \right)\]
(iii) \[y = a_1 \sin 2\omega t\]
(iv) \[y = a_2 \sin 2\left( \omega t + \epsilon \right).\]
Interference fringes may be observed due to superposition of
(a) (i) and (ii)
(b) (i) and (iii)
(c) (ii) and (iv)
(d) (iii) and (iv)
A narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror, as shown in the following figure. The light coming directly from the slit and that coming after the reflection interfere at a screen ∑ placed at a distance D from the slit. (a) What will be the intensity at a point just above the mirror, i.e. just above O? (b) At what distance from O does the first maximum occur?
The intensity at the central maximum (O) in a Young’s double slit experimental set-up shown in the figure is IO. If the distance OP equals one-third of the fringe width of the pattern, show that the intensity at point P, would equal `(I_0)/4`.

Answer the following question.
Describe any two characteristic features which distinguish between interference and diffraction phenomena. Derive the expression for the intensity at a point of the interference pattern in Young's double-slit experiment.
Answer in brief:
In Young's double-slit experiment what will we observe on the screen when white light is incident on the slits but one slit is covered with a red filter and the other with a violet filter? Give reasons for your answer.
The intensity of the light coming from one of the slits in Young's experiment is twice the intensity of the light coming from the other slit. What will be the approximate ratio of the intensities of the bright and dark fringes in the resulting interference pattern?
What is interference?
In a Young’s double-slit experiment, the slit separation is doubled. To maintain the same fringe spacing on the screen, the screen-to-slit distance D must be changed to ______.
One of Young’s double slits is covered with a glass plate as shown in figure. The position of central maximum will,
What is intensity (or) amplitude division?
Obtain the equation for resultant intensity due to interference of light.
Discuss the interference in thin films and obtain the equations for constructive and destructive interference for transmitted and reflected light.
Two independent monochromatic sources cannot act as coherent sources, why?
Does diffraction take place at Young’s double-slit?
In Young's double-slit experiment, if the width of the 2nd bright fringe is 4 x 10-2 cm, then the width of the 4th bright fringe will be ______ cm.
A graph is plotted between the fringe-width Z and the distance D between the slit and eye-piece, keeping other adjustment same. The correct graph is
A.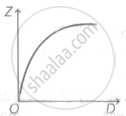 |
B. |
C.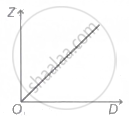 |
D.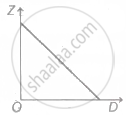 |
A metal rod has length, cross-sectional area and Young's modulus as L, A and Y, respectively. If the elongation in the rod produced is l, then work done is proportional to ______.
The light waves from two independent monochromatic light sources are given by, y1 = 2 sin ωt and y2 = 3 cos ωt. Then the correct statement is ____________.
In Young's experiment for the interference of light, the separation between the silts is d and the distance of the screen from the slits is D. If D is increased by 0.6% and d is decreased by 0.2%, then for the light of a given wavelength, which one of the following is true?
"The fringe width ____________."
In a Young's double-slit experiment, the intensity at a point where the path difference is `lambda/3` (`lambda` being the wavelength of the light used) is I. If I0 denotes the maximum intensity, then `"I"/"I"_0` is equal to ______.
A thin mica sheet of thickness 4 x 10-6 m and refractive index 1.5 is introduced in the path of the first wave. The wavelength of the wave used is 5000 A. The central bright maximum will shift ______.
In Young's double slit experiment the source is white light. One slit is covered with red filter and the other with blue filter. There shall be ____________.
The phenomenon of interference is based on ______.
Two coherent light sources of intensity ratio 'n' are employed in an interference experiment. The ratio of the intensities of the maxima and minima in the interference pattern is (I1 > I2).
In biprism experiment, if the 5th bright band with wavelength 'λ1' coincides with the 6th dark band with wavelength 'λ2' then the ratio `(lambda_2/lambda_1)` is ______
How will the interference pattern of Young's double slit change if one of the two slits is covered by a paper which transmits only half of the light intensity?
Two coherent sources P and Q produce interference at point A on the screen where there is a dark band which is formed between 4th bright band and 5th bright band. Wavelength of light used is 6000 Å. The path difference between PA and QA is ______.
