Advertisements
Advertisements
प्रश्न
Discuss the interference in thin films and obtain the equations for constructive and destructive interference for transmitted and reflected light.
उत्तर
- Interference in thin films:
- Let us consider a thin film of transparent material of refractive index p (not to confuse with an order of fringe n) and thickness d. A parallel beam of light is incident on the film at an angle i.
- The wave is divided into two parts at the upper surface, one is reflected and the other is refracted. The refracted part, which enters into the film, again gets divided at the lower surface into two parts; one is transmitted out of the film and the other is reflected back into the film.
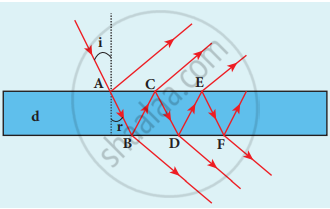
Interference in thin films
- For transmitted light:
- The light transmitted may interfere to produce a resultant intensity. Let us consider the path difference between the two light waves transmitted from B and D. The two waves moved together and remained in phase up to B where splitting occurred.
- The extra path travelled by the wave transmitted from D is the path inside the film, BC + CD. If we approximate the incidence to be nearly normal (i = 0), then points B and D are very close to each other. The extra distance travelled by the wave is approximately twice thickness of the film, BC + CD = 2d. As this extra path is travelled in a medium of refractive index p, the optical path difference is,
δ = 2μd. - The condition for constructive interference in transmitted ray is,
2μd = nλ
Similarly, the condition for destructive interference in transmitted ray is
2μd = (2n-l) `λ/2`
- For reflected light:
- Wave while travelling in a rarer medium and getting reflected by a denser medium, undergoes a phase change of n or an additional path difference of `λ/2`.
- Let us consider the path difference between the light waves reflected by the upper surface at A and the other wave coming out at C after passing through the film.
- The additional path travelled by wave coming out from C is the path inside the film, AB + BC. For nearly normal incidence this distance could be approximated as, AB + BC = 2d. As this extra path is travelled in the medium of refractive index p, the optical path difference is, δ = 2μd.
- The condition for constructive interference for reflected ray is,
2μd + `λ/2` = nλ (or)
2μd = (2n – 1) `λ/2` - The additional path difference λ/2 is due to the phase change of n in rarer to denser reflection taking place at A. The condition for destructive interference for a reflected ray is,
2μd + `λ/2` = (2n + l)`λ/2` (or)
2μd = nλ
APPEARS IN
संबंधित प्रश्न
Four light waves are represented by
(i) \[y = a_1 \sin \omega t\]
(ii) \[y = a_2 \sin \left( \omega t + \epsilon \right)\]
(iii) \[y = a_1 \sin 2\omega t\]
(iv) \[y = a_2 \sin 2\left( \omega t + \epsilon \right).\]
Interference fringes may be observed due to superposition of
(a) (i) and (ii)
(b) (i) and (iii)
(c) (ii) and (iv)
(d) (iii) and (iv)
A long narrow horizontal slit is paced 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 m away from the slit. If the mirror reflects only 64% of the light energy falling on it, what will be the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen?
Answer in brief:
In Young's double-slit experiment what will we observe on the screen when white light is incident on the slits but one slit is covered with a red filter and the other with a violet filter? Give reasons for your answer.
Two coherent sources whose intensity ratio is 25:1 produce interference fringes. Calculate the ratio of amplitudes of light waves coming from them.
How do source and images behave as coherent sources?
What is a bandwidth of interference pattern?
Light of wavelength 600 nm that falls on a pair of slits producing interference pattern on a screen in which the bright fringes are separated by 7.2 mm. What must be the wavelength of another light which produces bright fringes separated by 8.1 mm with the same apparatus?
The interference pattern is obtained with two coherent light sources of intensity ratio n. In the interference pattern, the ratio `("I"_"max" - "I"_"min")/("I"_"max" + "I"_"min")` will be ______
A graph is plotted between the fringe-width Z and the distance D between the slit and eye-piece, keeping other adjustment same. The correct graph is
A.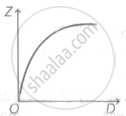 |
B. |
C.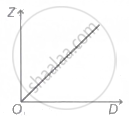 |
D.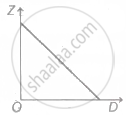 |
A metal rod has length, cross-sectional area and Young's modulus as L, A and Y, respectively. If the elongation in the rod produced is l, then work done is proportional to ______.
A thin mica sheet of thickness 4 x 10-6 m and refractive index 1.5 is introduced in the path of the first wave. The wavelength of the wave used is 5000 A. The central bright maximum will shift ______.
In a Young's experiment, two coherent sources are placed 0.60 mm apart and the fringes are observed one metre away. If it produces the second dark fringe at a distance of 1 mm from the central fringe, the wavelength of monochromatic light used would be ____________.
In Young's double slit experiment with a source of light of wavelength 5860 Å, the first maxima will occur when ____________.
In biprism experiment, the 4th dark band is formed opposite to one of the slits. The wavelength of light used is ______.
The graph shows the variation of fringe width (β) versus distance of the screen from the plane of the slits (D) in Young's double-slit experiment Keeping other parameters the same. The wavelength of light used can be calculated as d = distance between the slits ______

Two coherent sources of intensities I1 and I2 produce an interference pattern on the screen. The maximum intensity in the interference pattern is ______
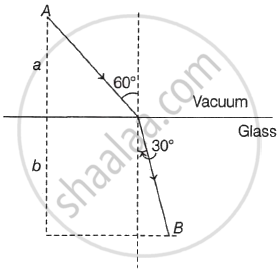
A ray of light AO in vacuum is incident on a glass slab at angle 60° and refracted at angle 30° along OB as shown in the figure. The optical path length of light ray from A to B is ______.
In a double-slit experiment, the optical path difference between the waves coming from two coherent sources at a point P on one side of the central bright is 7.5 µm and that at a point Q on the other side of the central bright fringe and 1.8 µm. How many bright and dark fringes are observed between points P and Q if the wavelength of light used is 600 nm?
