Advertisements
Advertisements
Question
Discuss the interference in thin films and obtain the equations for constructive and destructive interference for transmitted and reflected light.
Solution
- Interference in thin films:
- Let us consider a thin film of transparent material of refractive index p (not to confuse with an order of fringe n) and thickness d. A parallel beam of light is incident on the film at an angle i.
- The wave is divided into two parts at the upper surface, one is reflected and the other is refracted. The refracted part, which enters into the film, again gets divided at the lower surface into two parts; one is transmitted out of the film and the other is reflected back into the film.
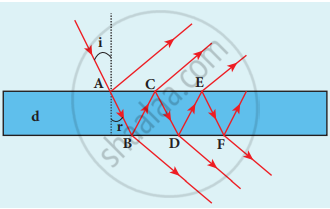
Interference in thin films
- For transmitted light:
- The light transmitted may interfere to produce a resultant intensity. Let us consider the path difference between the two light waves transmitted from B and D. The two waves moved together and remained in phase up to B where splitting occurred.
- The extra path travelled by the wave transmitted from D is the path inside the film, BC + CD. If we approximate the incidence to be nearly normal (i = 0), then points B and D are very close to each other. The extra distance travelled by the wave is approximately twice thickness of the film, BC + CD = 2d. As this extra path is travelled in a medium of refractive index p, the optical path difference is,
δ = 2μd. - The condition for constructive interference in transmitted ray is,
2μd = nλ
Similarly, the condition for destructive interference in transmitted ray is
2μd = (2n-l) `λ/2`
- For reflected light:
- Wave while travelling in a rarer medium and getting reflected by a denser medium, undergoes a phase change of n or an additional path difference of `λ/2`.
- Let us consider the path difference between the light waves reflected by the upper surface at A and the other wave coming out at C after passing through the film.
- The additional path travelled by wave coming out from C is the path inside the film, AB + BC. For nearly normal incidence this distance could be approximated as, AB + BC = 2d. As this extra path is travelled in the medium of refractive index p, the optical path difference is, δ = 2μd.
- The condition for constructive interference for reflected ray is,
2μd + `λ/2` = nλ (or)
2μd = (2n – 1) `λ/2` - The additional path difference λ/2 is due to the phase change of n in rarer to denser reflection taking place at A. The condition for destructive interference for a reflected ray is,
2μd + `λ/2` = (2n + l)`λ/2` (or)
2μd = nλ
APPEARS IN
RELATED QUESTIONS
Why are multiple colours observed over a thin film of oil floating on water? Explain with the help of a diagram.
Answer in brief:
Explain what is the optical path length. How is it different from actual path length?
What are the two methods for obtaining coherent sources in the laboratory?
The intensity of the light coming from one of the slits in Young's experiment is twice the intensity of the light coming from the other slit. What will be the approximate ratio of the intensities of the bright and dark fringes in the resulting interference pattern?
Why two light sources must be of equal intensity to obtain a well-defined interference pattern?
One of Young’s double slits is covered with a glass plate as shown in figure. The position of central maximum will,
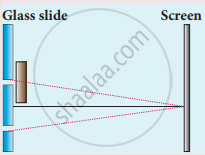
What is intensity (or) amplitude division?
Obtain the equation for bandwidth in Young’s double slit experiment.
Light of wavelength 600 nm that falls on a pair of slits producing interference pattern on a screen in which the bright fringes are separated by 7.2 mm. What must be the wavelength of another light which produces bright fringes separated by 8.1 mm with the same apparatus?
The interference pattern is obtained with two coherent light sources of intensity ratio n. In the interference pattern, the ratio `("I"_"max" - "I"_"min")/("I"_"max" + "I"_"min")` will be ______
A graph is plotted between the fringe-width Z and the distance D between the slit and eye-piece, keeping other adjustment same. The correct graph is
A.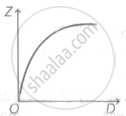 |
B. |
C.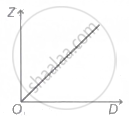 |
D.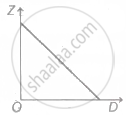 |
On a rainy day, a small oil film on water shows brilliant colours. This is due to ____________.
The phenomenon of interference is based on ______.
If two light waves reaching a point produce destructive interference, then the condition of phase difference is ______
Waves from two coherent sources of light having an intensity ratio I1 : I2 equal to 'x' interfere. Then in the interference pattern obtained on the screen, the value of (Imax - Imin)/(Imax + Imin) is ______
In a biprism experiment, monochromatic light of wavelength (λ) is used. The distance between two coherent sources is kept constant. If the distance between slit and eyepiece (D) is varied as D1, D2, D3, and D4, the corresponding measured fringe widths are z1, z2, z3, and z4 then ______
In the biprism experiment, a source of monochromatic light is used for a certain distance between slit and eyepiece. When the distance between two virtual sources is changed from dA to dB, then the fringe width is changed from ZA to ZB. The ratio ZA to ZB is ______
White light is passed through a double slit and interference is observed on a screen 1.5 m away. The separation between the slits is 0.3 mm. The first violet and red fringes are formed 2.0 mm and 3.5 mm away from the central white fringes. The difference in wavelengths of red and violet light is ______ nm.
In biprism experiment, the distance of 20th bright band from the central bright band is 1.2 cm. Without changing the experimental set-up, the distance of 30th bright band from the central bright band will be ______.
