Advertisements
Advertisements
Questions
Answer in brief:
Explain what is the optical path length. How is it different from actual path length?
What is Optical Path length? How is it different from the actual Path length?
Solution 1
Consider, a light wave with an angular frequency of w and a wave vector of k travelling in the x-direction through a vacuum. The phase of this wave is (kx - ωt). In a vacuum, light speed at c, but in a medium, it speeds at v.
k = `(2pi)/lambda = (2pi v)/(v lambda) = omega/v` as ω = 2πv and v = vλ, where v is the frequency of light.
If the wave travels a distance Δ x, its phase changes by Δ Φ = kΔx = ω Δx/v.
Similarly, if the wave is travelling in vacuum,
k = ω/c and Δ Φ = ω Δ x/c
Now, consider a wave travelling a distance Δ x in the medium, the phase difference generated is,
Δ Φ' = k' Δ x = ωn Δ x/c = ω Δ x'/c ...(1)
where Δ x' = n Δ x .....(2)
The distance nΔ x is called the optical path length of the light in the medium; it is the distance the light would have travelled in the same time t in vacuum (with the speed c).
The optical path length in a medium is the corresponding path in a vacuum that light traverses at the same time as it does in the medium.
Now, speed = `"distance"/"time"`
∴ time = `"distance"/"speed"`
∴ t = `"d"_"medium"/"v"_"medium" = "d"_"vaccum"/"v"_"vaccum"`
Hence, the optical path = `"d"_"vacuum"`
`= "v"_"vaccum"/"v"_"medium" xx "d"_"medium"`
`= "n" xx "d"_"medium"`
Thus, a distance d travelled in a medium of refractive index n introduces a path difference = nd - d = d (n - 1) over a ray travelling equal distance through vacuum.
Solution 2
i. When a wave travels a distance Δx through a medium having a refractive index of n, its phase changes by the same amount as it would if the wave had travelled a distance nΔx in a vacuum.
ii. Thus, a path length of Δx in a medium of refractive index n is equivalent to a path length of nΔx in a vacuum.
iii. nΔx is called the optical path travelled by a wave.
iv. This means, the optical path through a medium is the effective path travelled by light in a vacuum to generate the same phase difference.
v. Optical path in a medium can also be defined as the corresponding path in a vacuum that the light travels at the same time as it takes in the given medium.
i.e., time = `"d"_"medium"/"v"_"medium" = "d"_"vacuum"/"v"_"vacuum"`
∴ `"d"_"vacuum" = "v"_"vacuum"/"v"_"medium" xx "d"_"medium" = "n" xx "d"_"medium"`
But `"d"_"vacuum"` = Optical path
∴ Optical path = n × `"d"_"medium"`
Thus, a distance d travelled in a medium of refractive index n introduces a path difference = nd - d = d(n - 1) over a ray travelling an equal distance through the vacuum.
RELATED QUESTIONS
Write the important characteristic features by which the interference can be distinguished from the observed diffraction pattern.
Write the necessary conditions to obtain sustained interference fringes.
A narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror, as shown in the following figure. The light coming directly from the slit and that coming after the reflection interfere at a screen ∑ placed at a distance D from the slit. (a) What will be the intensity at a point just above the mirror, i.e. just above O? (b) At what distance from O does the first maximum occur?
A long narrow horizontal slit is paced 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 m away from the slit. Find the fringe-width if the light used has a wavelength of 700 nm.
Why are multiple colours observed over a thin film of oil floating on water? Explain with the help of a diagram.
Answer in brief:
What is meant by coherent sources?
Answer in brief:
In Young's double-slit experiment what will we observe on the screen when white light is incident on the slits but one slit is covered with a red filter and the other with a violet filter? Give reasons for your answer.
Describe Young's double-slit interference experiment and derive conditions for occurrence of dark and bright fringes on the screen. Define fringe width and derive a formula for it.
What are the conditions for obtaining a good interference pattern? Give reasons.
A double-slit arrangement produces interference fringes for sodium light (λ = 589 nm) that are 0.20° apart. What is the angular fringe separation if the entire arrangement is immersed in water (n = 1.33)?
The intensity of the light coming from one of the slits in Young's experiment is twice the intensity of the light coming from the other slit. What will be the approximate ratio of the intensities of the bright and dark fringes in the resulting interference pattern?
In a Young’s double-slit experiment, the slit separation is doubled. To maintain the same fringe spacing on the screen, the screen-to-slit distance D must be changed to ______.
Obtain the relation between phase difference and path difference.
What is intensity (or) amplitude division?
In Young’s double-slit experiment, 62 fringes are seen in the visible region for sodium light of wavelength 5893 Å. If violet light of wavelength 4359 Å is used in place of sodium light, then what is the number of fringes seen?
In Young's double-slit experiment, if the width of the 2nd bright fringe is 4 x 10-2 cm, then the width of the 4th bright fringe will be ______ cm.
In Young's double slit experiment green light is incident on the two slits. The interference pattern is observed on a screen. Which one of the following changes would cause the observed fringes to be more closely spaced?
In Young's double-slit experiment, in an interference pattern, a second minimum is observed exactly in front of one slit. The distance between the two coherent sources is 'd' and the distance between source and screen is 'D'. The wavelength of the light source used is ______
A wire of length 'L' and area of cross-section · A' is made of material of Young's modulus 'Y'. It is stretched by an amount 'x'. The work done in stretching the wire is ______.
In Young's experiment for the interference of light, the separation between the silts is d and the distance of the screen from the slits is D. If D is increased by 0.6% and d is decreased by 0.2%, then for the light of a given wavelength, which one of the following is true?
"The fringe width ____________."
In Young's experiment, the distance between the slits is doubled and the distance between the slit and screen is reduced to half, then the fringe width ____________.
In a biprism experiment, red light of wavelength 6500 Å was used. It was then replaced by green light of wavelength 5200 Å. The value of n for which (n + 1)th green bright band would coincide with nth red bright band for the same setting is ______.
In the Young's double slit experiment, if the phase difference between the two waves interfering at a point is `phi`, the intensity at that point is proportional to ____________.
In a biprism experiment, monochromatic light of wavelength (λ) is used. The distance between two coherent sources is kept constant. If the distance between slit and eyepiece (D) is varied as D1, D2, D3, and D4, the corresponding measured fringe widths are z1, z2, z3, and z4 then ______
In an interference experiment, the intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at ____________.
(cos 60° = 0.5, `lambda` = wavelength of light, d = slit width)
The interference pattern is obtained with two coherent light sources of intensity ratio 4 : 1. And the ratio `("I"_"max" - "I"_"min")/("I"_"max" + "I"_"min")` is `5/x`. Then the value of x will be equal to ______.
The path difference between two interference light waves meeting at a point on the screen is `(87/2)lambda`. The band obtained at that point is ______.
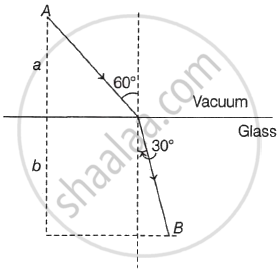
A ray of light AO in vacuum is incident on a glass slab at angle 60° and refracted at angle 30° along OB as shown in the figure. The optical path length of light ray from A to B is ______.
In a double-slit experiment, the optical path difference between the waves coming from two coherent sources at a point P on one side of the central bright is 7.5 µm and that at a point Q on the other side of the central bright fringe and 1.8 µm. How many bright and dark fringes are observed between points P and Q if the wavelength of light used is 600 nm?
