Advertisements
Advertisements
Question
Describe Young's double-slit interference experiment and derive conditions for occurrence of dark and bright fringes on the screen. Define fringe width and derive a formula for it.
Solution
Description of Young's double-slit interference experiment:
- a plane wavefront is made to fall on an opaque screen AB having two similar narrow slits S1 and S2.
- The plane wavefront can be either obtained by placing a linear source S far away from the screen or by placing it at the focus of a convex lens kept close to AB.
- The rays coming out of the lens will be parallel rays and the wavefront will be a plane wave front as shown in Figure.
- The figure shows a cross-section of the experimental set up and the slits have their lengths perpendicular to the plane of the paper. For better results, the slits should be about 2-4 mm apart from each other. An observing screen PQ is placed behind of AB.
- For simplicity, we assume that the slits S1 and S2 are equidistant from the S so that the wavefronts starting from S and reaching the S1 and S2 at every instant of time are in phase.

Young's double-slit experiment - S1 and S2 act as secondary sources. The crests/troughs of the secondary wavelets superpose and interfere constructively along straight lines joining the black dots shown in the above figure. The point where these lines meet the screen have high intensity and is bright.
- Similarly, there are points shown with red dots where the crest of one wave coincides with the trough of the other. The corresponding points on the screen are dark due to destructive interference. These dark and bright regions are called fringes or bands and the whole pattern is called an interference pattern.
Conditions for the occurrence of dark and bright lunges on the screen:
Consider Young's double-slit experimental set up. Wavefront splitting produces two narrow coherent light sources as monochromatic light of wavelength emerges from two narrow and closely spaced, parallel slits S1 and S2 of equal widths. The separation S1 S2 = d is very small. The interference pattern is observed on a screen placed parallel to the plane of S1S2 and at a considerable distance D (D >> d) from the slits. OO' is the perpendicular bisector of a segment S1S2.
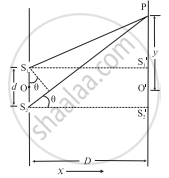
Geometry of the double-slit experiment
Consider, a point P on the screen at a distance y from O' (y << 0). The two light waves from S1 and S2 reach P along paths S1P and S2P, respectively. If the path difference (Δl) between S1P and S2P is an integral multiple of λ, the two waves arriving there will interfere constructively producing a bright fringe at P. On the contrary, if the path difference between S1P and S2P is a half-integral multiple of λ, there will be destructive interference and a dark fringe will be produced at P.
From the above figure,
(S2P)2 = (S2S2')2 + (PS2')2
= (S2S2')2 + (PO' + O'S2')2
`= "D"^2 + ("y" + "d"/2)^2` ....(1)
and (S1P)2 = (S1S1')2 + (PS1')2
= (S1S1')2 + (PQ' - Q'S1)2
= `"D"^2 + ("y" - "d"/2)^2` .....(2)
(S2P)2 - (S1P)2 = `{"D"^2 + ("y" + "d"/2)^2} - {"D"^2 + ("y" - "d"/2)^2}`
∴ (S2P + S1P)(S2P - S1P)
`= ["D"^2 + "y"^2 + "d"^2/4 + "yd"] - ["D"^2 + "y"^2 + "d"^2/4 - "yd"] = 2"yd"`
∴ S2P + S1P = Δ l = 2yd/S2P + S1P
In practice, D >> y and D >> d,
∴ S2P + S1P ≅ 2D
∴ Path difference,
Δ l = S2P + S1P ≅ 2 `"yd"/"2D" = "y" "d"/"D"` ....(3)
The expression for the fringe width (or band width):
The distance between consecutive bright (or dark) fringes is called the fringe width (or bandwidth) W. Point P will be bright (maximum intensity), if the
path difference, Δ l = `"y"_"n" "d"/"D" = "n" lambda` where n = 0, 1, 2, 3, .....
Point P will be dark (minimum intensity equal to zero), if `"y"_"m" "d"/"D" = ("2m" - 1) lambda/2`, where, m = 1,2,3...,
Thus, for bright fringes (or bands),
`"y"_"n" = 0, lambda "D"/"d", (2lambda"D")/"d"` ...
and for dark fringes (or bands),
`"y"_"n" = lambda/2 "D"/"d", 3 lambda/2 "D"/"d", 5lambda/2 "D"/"d"` ....
The bright and dark fringes (or bands) alternate and are evenly spaced in these situations. For Point O', the path difference (S2O' - S1O') = 0. Hence, point O' will be bright. It corresponds to the centre of the central bright fringe (or band). On both sides of O', the interference pattern consists of alternate dark and bright fringes (or band) parallel to the slit.
Let `"y"_"n"` and `"y"_"n + 1"`, be the distances of the nth and (m + 1)th bright fringes from the central bright fringe.
∴ `("y"_"n""d")/"D" = "n" lambda`
∴ `"y"_"n" = ("n" lambda "D")/"d"` .....(4)
and `("y"_("n + 1")"d")/"D" = ("n + 1")lambda`
∴ `("y"_("n + 1")) = (("n + 1") lambda "D")/"d"` .....(5)
The distance between consecutive bright fringes
`= "y"_("n + 1") - "y"_"n" = (lambda "D")/"d" [("n + 1") - "n"] = (lambda"D")/"d"` ....(6)
Hence, the fringe width,
∴ W = `triangle "y" = "y"_("n + 1") - "y"_"n" = (lambda"D")/"d"` (for bright fringes) ... (7)
Alternately, let `"y"_"m"` and `"y"_"m + 1"` be the distances of the m th and (m + 1)th dark fringes respectively from the central bright fringe.
∴ `("y"_"m""d")/"D" = (2"m" - 1) lambda/2` and
`("y"_("m+1")"d")/"D" = [2("m + 1") - 1] lambda/2 = (2"m" + 1) lambda/2` ....(8)
∴ `"y"_"m" = (2"m - 1") (lambda"D")/"2d"` and
`"y"_"m + 1" = (2"m" + 1) (lambda"D")/"2d"` .....(9)
∴ The distance between consecutive dark fringes,
`"y"_"m + 1" - "y"_"m" = (lambda"D")/"2d" [(2"m" + 1) - (2"m" - 1)] = (lambda"D")/"d"` ....(10)
∴ W = `"y"_"m + 1" - "y"_"m"`
`= (lambda"D")/"d"` (for dark fringes) .....(11)
Eqs. (7) and (11) show that the fringe width is the same for bright and dark fringes.
RELATED QUESTIONS
State any one difference between interference of light and diffraction of light
When a drop of oil is spread on a water surface, it displays beautiful colours in daylight because of ______________ .
The intensity at the central maximum (O) in a Young’s double slit experimental set-up shown in the figure is IO. If the distance OP equals one-third of the fringe width of the pattern, show that the intensity at point P, would equal `(I_0)/4`.

Why two light sources must be of equal intensity to obtain a well-defined interference pattern?
Obtain the relation between phase difference and path difference.
What is a bandwidth of interference pattern?
Obtain the equation for bandwidth in Young’s double slit experiment.
Does diffraction take place at Young’s double-slit?
In Young’s double slit experiment, the slits are 2 mm apart and are illuminated with a mixture of two wavelength λ0 = 750 nm and λ = 900 nm. What is the minimum distance from the common central bright fringe on a screen 2 m from the slits where a bright fringe from one interference pattern coincides with a bright fringe from the other?
The ratio of maximum and minimum intensities in an interference pattern is 36 : 1. What is the ratio of the amplitudes of the two interfering waves?
Light of wavelength 600 nm that falls on a pair of slits producing interference pattern on a screen in which the bright fringes are separated by 7.2 mm. What must be the wavelength of another light which produces bright fringes separated by 8.1 mm with the same apparatus?
The interference pattern is obtained with two coherent light sources of intensity ratio n. In the interference pattern, the ratio `("I"_"max" - "I"_"min")/("I"_"max" + "I"_"min")` will be ______
The distance between the first and ninth bright fringes formed in a biprism experiment is ______.
(`lambda` = 6000 A, D = 1.0 m, d = 1.2 mm)
In Young's experiment for the interference of light, the separation between the silts is d and the distance of the screen from the slits is D. If D is increased by 0.6% and d is decreased by 0.2%, then for the light of a given wavelength, which one of the following is true?
"The fringe width ____________."
In Young's experiment, the distance between the slits is doubled and the distance between the slit and screen is reduced to half, then the fringe width ____________.
In a biprism experiment, D = 1 m, `lambda` = 6000 Å. When a convex lens is interposed between the biprism ru1d the eyepiece, then the distance between the images of the slits given by the Jens at two positions are 1.5 mm and 6.0 mm. The fringe width will be ______.
A thin mica sheet of thickness 4 x 10-6 m and refractive index 1.5 is introduced in the path of the first wave. The wavelength of the wave used is 5000 A. The central bright maximum will shift ______.
In Young's double slit experiment the source is white light. One slit is covered with red filter and the other with blue filter. There shall be ____________.
The phenomenon of interference is based on ______.
In a biprism experiment, red light of wavelength 6500 Å was used. It was then replaced by green light of wavelength 5200 Å. The value of n for which (n + 1)th green bright band would coincide with nth red bright band for the same setting is ______.
`phi "and" phi_2 (phi_1 > phi_2)` are the work functions of metals A and B. When light of same wavelength is incident on A and B, the fastest emitted electrons from A are ____________ those emitted from B.
In a biprism experiment, the slit separation is 1 mm. Using monochromatic light of wavelength 5000 Å, an interference pattern is obtained on the screen. Where should the screen be moved? so that the change in fringe width is 12.5 x 105 m?
In Young's double-slit experiment, the distance between the slits is 3 mm and the slits are 2 m away from the screen. Two interference patterns can be obtained on the screen due to light of wavelength 480 nm and 600 run respectively. The separation on the screen between the 5th order bright fringes on the two interference patterns is ______
In Young's double-slit experiment, the distance between the slits is 3 mm and the slits are 2 m away from the screen. Two interference patterns can be obtained on the screen due to light of wavelength 480 nm and 600 run respectively. The separation on the screen between the 5th order bright fringes on the two interference patterns is ______
What is meant by Constructive interference?
The path difference between two interference light waves meeting at a point on the screen is `(87/2)lambda`. The band obtained at that point is ______.
