Advertisements
Advertisements
प्रश्न
Describe Young's double-slit interference experiment and derive conditions for occurrence of dark and bright fringes on the screen. Define fringe width and derive a formula for it.
उत्तर
Description of Young's double-slit interference experiment:
- a plane wavefront is made to fall on an opaque screen AB having two similar narrow slits S1 and S2.
- The plane wavefront can be either obtained by placing a linear source S far away from the screen or by placing it at the focus of a convex lens kept close to AB.
- The rays coming out of the lens will be parallel rays and the wavefront will be a plane wave front as shown in Figure.
- The figure shows a cross-section of the experimental set up and the slits have their lengths perpendicular to the plane of the paper. For better results, the slits should be about 2-4 mm apart from each other. An observing screen PQ is placed behind of AB.
- For simplicity, we assume that the slits S1 and S2 are equidistant from the S so that the wavefronts starting from S and reaching the S1 and S2 at every instant of time are in phase.

Young's double-slit experiment - S1 and S2 act as secondary sources. The crests/troughs of the secondary wavelets superpose and interfere constructively along straight lines joining the black dots shown in the above figure. The point where these lines meet the screen have high intensity and is bright.
- Similarly, there are points shown with red dots where the crest of one wave coincides with the trough of the other. The corresponding points on the screen are dark due to destructive interference. These dark and bright regions are called fringes or bands and the whole pattern is called an interference pattern.
Conditions for the occurrence of dark and bright lunges on the screen:
Consider Young's double-slit experimental set up. Wavefront splitting produces two narrow coherent light sources as monochromatic light of wavelength emerges from two narrow and closely spaced, parallel slits S1 and S2 of equal widths. The separation S1 S2 = d is very small. The interference pattern is observed on a screen placed parallel to the plane of S1S2 and at a considerable distance D (D >> d) from the slits. OO' is the perpendicular bisector of a segment S1S2.
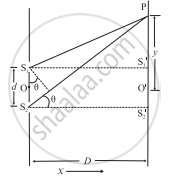
Geometry of the double-slit experiment
Consider, a point P on the screen at a distance y from O' (y << 0). The two light waves from S1 and S2 reach P along paths S1P and S2P, respectively. If the path difference (Δl) between S1P and S2P is an integral multiple of λ, the two waves arriving there will interfere constructively producing a bright fringe at P. On the contrary, if the path difference between S1P and S2P is a half-integral multiple of λ, there will be destructive interference and a dark fringe will be produced at P.
From the above figure,
(S2P)2 = (S2S2')2 + (PS2')2
= (S2S2')2 + (PO' + O'S2')2
`= "D"^2 + ("y" + "d"/2)^2` ....(1)
and (S1P)2 = (S1S1')2 + (PS1')2
= (S1S1')2 + (PQ' - Q'S1)2
= `"D"^2 + ("y" - "d"/2)^2` .....(2)
(S2P)2 - (S1P)2 = `{"D"^2 + ("y" + "d"/2)^2} - {"D"^2 + ("y" - "d"/2)^2}`
∴ (S2P + S1P)(S2P - S1P)
`= ["D"^2 + "y"^2 + "d"^2/4 + "yd"] - ["D"^2 + "y"^2 + "d"^2/4 - "yd"] = 2"yd"`
∴ S2P + S1P = Δ l = 2yd/S2P + S1P
In practice, D >> y and D >> d,
∴ S2P + S1P ≅ 2D
∴ Path difference,
Δ l = S2P + S1P ≅ 2 `"yd"/"2D" = "y" "d"/"D"` ....(3)
The expression for the fringe width (or band width):
The distance between consecutive bright (or dark) fringes is called the fringe width (or bandwidth) W. Point P will be bright (maximum intensity), if the
path difference, Δ l = `"y"_"n" "d"/"D" = "n" lambda` where n = 0, 1, 2, 3, .....
Point P will be dark (minimum intensity equal to zero), if `"y"_"m" "d"/"D" = ("2m" - 1) lambda/2`, where, m = 1,2,3...,
Thus, for bright fringes (or bands),
`"y"_"n" = 0, lambda "D"/"d", (2lambda"D")/"d"` ...
and for dark fringes (or bands),
`"y"_"n" = lambda/2 "D"/"d", 3 lambda/2 "D"/"d", 5lambda/2 "D"/"d"` ....
The bright and dark fringes (or bands) alternate and are evenly spaced in these situations. For Point O', the path difference (S2O' - S1O') = 0. Hence, point O' will be bright. It corresponds to the centre of the central bright fringe (or band). On both sides of O', the interference pattern consists of alternate dark and bright fringes (or band) parallel to the slit.
Let `"y"_"n"` and `"y"_"n + 1"`, be the distances of the nth and (m + 1)th bright fringes from the central bright fringe.
∴ `("y"_"n""d")/"D" = "n" lambda`
∴ `"y"_"n" = ("n" lambda "D")/"d"` .....(4)
and `("y"_("n + 1")"d")/"D" = ("n + 1")lambda`
∴ `("y"_("n + 1")) = (("n + 1") lambda "D")/"d"` .....(5)
The distance between consecutive bright fringes
`= "y"_("n + 1") - "y"_"n" = (lambda "D")/"d" [("n + 1") - "n"] = (lambda"D")/"d"` ....(6)
Hence, the fringe width,
∴ W = `triangle "y" = "y"_("n + 1") - "y"_"n" = (lambda"D")/"d"` (for bright fringes) ... (7)
Alternately, let `"y"_"m"` and `"y"_"m + 1"` be the distances of the m th and (m + 1)th dark fringes respectively from the central bright fringe.
∴ `("y"_"m""d")/"D" = (2"m" - 1) lambda/2` and
`("y"_("m+1")"d")/"D" = [2("m + 1") - 1] lambda/2 = (2"m" + 1) lambda/2` ....(8)
∴ `"y"_"m" = (2"m - 1") (lambda"D")/"2d"` and
`"y"_"m + 1" = (2"m" + 1) (lambda"D")/"2d"` .....(9)
∴ The distance between consecutive dark fringes,
`"y"_"m + 1" - "y"_"m" = (lambda"D")/"2d" [(2"m" + 1) - (2"m" - 1)] = (lambda"D")/"d"` ....(10)
∴ W = `"y"_"m + 1" - "y"_"m"`
`= (lambda"D")/"d"` (for dark fringes) .....(11)
Eqs. (7) and (11) show that the fringe width is the same for bright and dark fringes.
संबंधित प्रश्न
How does the angular separation between fringes in single-slit diffraction experiment change when the distance of separation between the slit screens is doubled?
A long narrow horizontal slit is paced 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 m away from the slit. Find the fringe-width if the light used has a wavelength of 700 nm.
What are the conditions for obtaining a good interference pattern? Give reasons.
Two coherent sources whose intensity ratio is 25:1 produce interference fringes. Calculate the ratio of amplitudes of light waves coming from them.
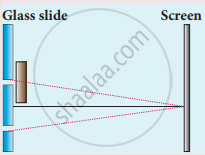
One of Young’s double slits is covered with a glass plate as shown in figure. The position of central maximum will,
Obtain the relation between phase difference and path difference.
How does wavefront division provide coherent sources?
How do source and images behave as coherent sources?
Does diffraction take place at Young’s double-slit?
In Young's double-slit experiment, in an interference pattern, a second minimum is observed exactly in front of one slit. The distance between the two coherent sources is 'd' and the distance between source and screen is 'D'. The wavelength of the light source used is ______
Two identical light waves having phase difference 'Φ' propagate in same direction. When they superpose, the intensity of the resultant wave is proportional to ______.
In Young's double slit experiment, the two slits act as coherent sources of equal amplitude A and wavelength `lambda`. In another experiment with the same set up the two slits are of equal amplitude A and wavelength `lambda`. but are incoherent. The ratio of the intensity of light at the mid-point of the screen in the first case to that in the second case is ____________.
In Young's double slit experiment the source is white light. One slit is covered with red filter and the other with blue filter. There shall be ____________.
In a biprism experiment, red light of wavelength 6500 Å was used. It was then replaced by green light of wavelength 5200 Å. The value of n for which (n + 1)th green bright band would coincide with nth red bright band for the same setting is ______.
If the two slits in Young's double slit experiment have width ratio 9 : 1, the ratio of maximum to minimum intensity in the interference pattern is ______.
In the Young's double slit experiment, if the phase difference between the two waves interfering at a point is `phi`, the intensity at that point is proportional to ____________.
In a double slit experiment, the separation between the slits is d and distance of screen from slits is D. If the wavelength of light used is `lambda` and I is the intensity of central bright fringe, then intensity at distance x from central maximum is given by ____________.
Two identical light sources s1 and s2 emit light of same wavelength `lambda`. These light rays will exhibit interference if their ______.
`phi "and" phi_2 (phi_1 > phi_2)` are the work functions of metals A and B. When light of same wavelength is incident on A and B, the fastest emitted electrons from A are ____________ those emitted from B.
In a biprism experiment, the slit separation is 1 mm. Using monochromatic light of wavelength 5000 Å, an interference pattern is obtained on the screen. Where should the screen be moved? so that the change in fringe width is 12.5 x 105 m?
Light waves from two coherent sources arrive at two points on a screen with a path difference of zero and λ/2. The ratio of the intensities at the points is ______
A double slit experiment is immersed in water of refractive index 1.33. The slit separation is 1 mm, distance between slit and screen is 1.33 m. The slits are illuminated by a light of wavelength 6300 Å. The fringe width is ______.
In Young's double-slit experiment, the distance between the slits is 3 mm and the slits are 2 m away from the screen. Two interference patterns can be obtained on the screen due to light of wavelength 480 nm and 600 run respectively. The separation on the screen between the 5th order bright fringes on the two interference patterns is ______
A beam of electrons is used in Young's double-slit experiment. If the speed of electrons is increased then the fringe width will ______.
The path difference between two interference light waves meeting at a point on the screen is `(87/2)lambda`. The band obtained at that point is ______.
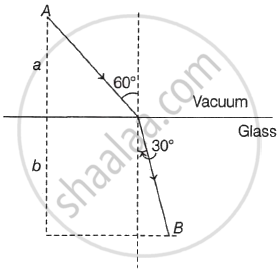
A ray of light AO in vacuum is incident on a glass slab at angle 60° and refracted at angle 30° along OB as shown in the figure. The optical path length of light ray from A to B is ______.
In a double-slit experiment, the optical path difference between the waves coming from two coherent sources at a point P on one side of the central bright is 7.5 µm and that at a point Q on the other side of the central bright fringe and 1.8 µm. How many bright and dark fringes are observed between points P and Q if the wavelength of light used is 600 nm?
