Advertisements
Advertisements
प्रश्न
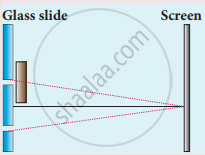
A long narrow horizontal slit is paced 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 m away from the slit. Find the fringe-width if the light used has a wavelength of 700 nm.
उत्तर
Given:-
Separation between two slits, \[d' = 2d = 2 mm = 2 \times {10}^{- 3} m..........\left(\text{as d = 1 mm}\right)\]
Wavelength of the light used,
\[\lambda = 700 nm = 700 \times {10}^{- 3} m\]
Distance between the screen and slit (D) = 1.0 m
It is a case of Lloyd's mirror experiment.
\[\text{Fringe width, }\beta = \frac{\lambda D}{d'}\]
\[ = \frac{700 \times {10}^{- 9} \times 1}{2 \times {10}^{- 3}}\]
\[ = 0 . 35 \times {10}^{- 3} m = 0 . 35\text{ mm}\]
Hence, the width of the fringe is 0.35 mm.
APPEARS IN
संबंधित प्रश्न
A narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror, as shown in the following figure. The light coming directly from the slit and that coming after the reflection interfere at a screen ∑ placed at a distance D from the slit. (a) What will be the intensity at a point just above the mirror, i.e. just above O? (b) At what distance from O does the first maximum occur?
Two coherent sources whose intensity ratio is 25:1 produce interference fringes. Calculate the ratio of amplitudes of light waves coming from them.
Explain constructive and destructive interference with the help of a diagram?
One of Young’s double slits is covered with a glass plate as shown in figure. The position of central maximum will,
The interference pattern is obtained with two coherent light sources of intensity ratio n. In the interference pattern, the ratio `("I"_"max" - "I"_"min")/("I"_"max" + "I"_"min")` will be ______
A graph is plotted between the fringe-width Z and the distance D between the slit and eye-piece, keeping other adjustment same. The correct graph is
A.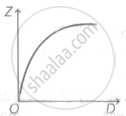 |
B. |
C.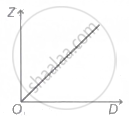 |
D.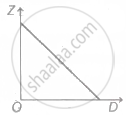 |
A thin transparent sheet is placed in front of a slit in Young's double slit experiment. The fringe width will ____________.
Two identical light waves having phase difference 'Φ' propagate in same direction. When they superpose, the intensity of the resultant wave is proportional to ______.
In Young's experiment, the distance between the slits is doubled and the distance between the slit and screen is reduced to half, then the fringe width ____________.
In Young's double-slit experiment, an interference pattern is obtained on a screen by a light of wavelength 4000 Å, coming from the coherent sources S1 and S2 At certain point P on the screen, third dark fringe is formed. Then the path difference S1P - S2P in microns is ______.
In Young's double slit experiment fifth dark fringe is formed opposite to one of the slits. If D is the distance between the slits and the screen and d is the separation between the slits, then the wavelength of light used is ______.
If two waves represented by `"y"_1 = 3 "sin" omega "t"` and `"y"_2 = 5 "sin" (omega "t" + pi/3)` interfere at a point, then the amplitude of the resulting wave will be about ____________.
`phi "and" phi_2 (phi_1 > phi_2)` are the work functions of metals A and B. When light of same wavelength is incident on A and B, the fastest emitted electrons from A are ____________ those emitted from B.
In the biprism experiment, a source of monochromatic light is used for a certain distance between slit and eyepiece. When the distance between two virtual sources is changed from dA to dB, then the fringe width is changed from ZA to ZB. The ratio ZA to ZB is ______
In Young's double-slit experiment, the distance between the slits is 3 mm and the slits are 2 m away from the screen. Two interference patterns can be obtained on the screen due to light of wavelength 480 nm and 600 run respectively. The separation on the screen between the 5th order bright fringes on the two interference patterns is ______
If we have two coherent sources S1 and S2 vibrating in phase, then for an arbitrary point P constructive interference is observed whenever the path difference is ______.
How will the interference pattern of Young's double slit change if one of the two slits is covered by a paper which transmits only half of the light intensity?
The path difference between two interference light waves meeting at a point on the screen is `(87/2)lambda`. The band obtained at that point is ______.
