Advertisements
Advertisements
प्रश्न
A narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror, as shown in the following figure. The light coming directly from the slit and that coming after the reflection interfere at a screen ∑ placed at a distance D from the slit. (a) What will be the intensity at a point just above the mirror, i.e. just above O? (b) At what distance from O does the first maximum occur?
उत्तर
(a) The phase of a light wave reflecting from a surface differs by \[\pi\] from the light directly coming from the source.
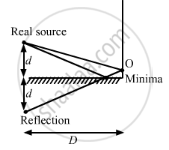
Thus, the wave fronts reaching just above the mirror directly from the source and after reflecting from the mirror have a phase difference of \[\pi,\] which is the condition of distractive interference. So, the intensity at a point just above the mirror is zero.
(b) Here, separation between two slits is 2d.
Wavelength of the light is `lambda.`
Distance of the screen from the slit is `D.`
Consider that the bright fringe is formed at position y. Then,
path difference, \[∆ x = \frac{y \times 2d}{D} = n\lambda.\]
After reflection from the mirror, path difference between two waves is \[\frac{\lambda}{2}.\]
\[\Rightarrow \frac{y \times 2d}{D} = \frac{\lambda}{2} + n\lambda\]
For first order, put n = 0
\[ \Rightarrow y = \frac{\lambda D}{4d}\]
APPEARS IN
संबंधित प्रश्न
Answer the following question.
Describe any two characteristic features which distinguish between interference and diffraction phenomena. Derive the expression for the intensity at a point of the interference pattern in Young's double-slit experiment.
Answer in brief:
In Young's double-slit experiment what will we observe on the screen when white light is incident on the slits but one slit is covered with a red filter and the other with a violet filter? Give reasons for your answer.
What are the conditions for obtaining a good interference pattern? Give reasons.
Describe geometry of the Young’s double slit experiment with the help of a ray diagram. What is fringe width? Obtain an expression of it. Write the conditions for constructive as well as destructive interference.
One of Young’s double slits is covered with a glass plate as shown in figure. The position of central maximum will,
Obtain the relation between phase difference and path difference.
A metal rod has length, cross-sectional area and Young's modulus as L, A and Y, respectively. If the elongation in the rod produced is l, then work done is proportional to ______.
A thin transparent sheet is placed in front of a slit in Young's double slit experiment. The fringe width will ____________.
A wire of length 'L' and area of cross-section · A' is made of material of Young's modulus 'Y'. It is stretched by an amount 'x'. The work done in stretching the wire is ______.
In a double slit experiment, the two slits are 2 mm apart and the screen is placed 1 m away. A monochromatic light of wavelength 500 nm is used. What will be the width of each slit for obtaining ten maxima of double slit within the central maxima of single slit pattern?
In Young's double slit experiment with a source of light of wavelength 5860 Å, the first maxima will occur when ____________.
The phenomenon of interference is based on ______.
In a biprism experiment, red light of wavelength 6500 Å was used. It was then replaced by green light of wavelength 5200 Å. The value of n for which (n + 1)th green bright band would coincide with nth red bright band for the same setting is ______.
In the Young's double slit experiment, if the phase difference between the two waves interfering at a point is `phi`, the intensity at that point is proportional to ____________.
Waves from two coherent sources of light having an intensity ratio I1 : I2 equal to 'x' interfere. Then in the interference pattern obtained on the screen, the value of (Imax - Imin)/(Imax + Imin) is ______
In Young's double slit experiment, for wavelength λ1 the nth bright fringe is obtained at a point P on the screen. Keeping the same setting, source of light is replaced by wavelength λ2 and now (n + 1)th bright fringe is obtained at the same point P on the screen. The value of n is ______.
If we have two coherent sources S1 and S2 vibrating in phase, then for an arbitrary point P constructive interference is observed whenever the path difference is ______.
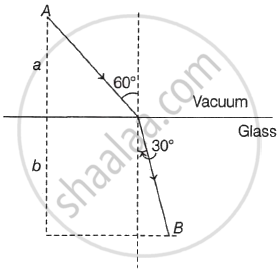
A ray of light AO in vacuum is incident on a glass slab at angle 60° and refracted at angle 30° along OB as shown in the figure. The optical path length of light ray from A to B is ______.
With a neat labelled ray diagram explain the use of Fresnel's biprism to obtain two coherent sources.
