Advertisements
Advertisements
प्रश्न
Two coherent sources whose intensity ratio is 25:1 produce interference fringes. Calculate the ratio of amplitudes of light waves coming from them.
उत्तर
`("I"_1)/("I"_2) = 25/1 = "a"_1^2/"a"_2^2 ⇒ "a"_1/"a"_2 = 5/1`
APPEARS IN
संबंधित प्रश्न
Laser light of wavelength 630 nm is incident on a pair of slits which are separated by 1.8 mm. If the screen is kept 80 cm away from the two slits, calculate:
1) fringe separation i.e. fringe width.
2) distance of 10th bright fringe from the centre of the interference pattern
How does the angular separation between fringes in single-slit diffraction experiment change when the distance of separation between the slit screens is doubled?
In Young’s double slit experiment, the slits are separated by 0.5 mm and screen is placed 1.0 m away from the slit. It is found that the 5th bright fringe is at a distance of 4.13 mm from the 2nd dark fringe. Find the wavelength of light used.
What are the conditions for obtaining a good interference pattern? Give reasons.
A double-slit arrangement produces interference fringes for sodium light (λ = 589 nm) that are 0.20° apart. What is the angular fringe separation if the entire arrangement is immersed in water (n = 1.33)?
Describe geometry of the Young’s double slit experiment with the help of a ray diagram. What is fringe width? Obtain an expression of it. Write the conditions for constructive as well as destructive interference.
Explain constructive and destructive interference with the help of a diagram?
One of Young’s double slits is covered with a glass plate as shown in figure. The position of central maximum will,
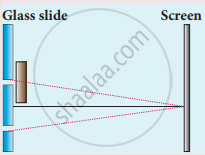
How do source and images behave as coherent sources?
Light of wavelength 600 nm that falls on a pair of slits producing interference pattern on a screen in which the bright fringes are separated by 7.2 mm. What must be the wavelength of another light which produces bright fringes separated by 8.1 mm with the same apparatus?
The interference pattern is obtained with two coherent light sources of intensity ratio n. In the interference pattern, the ratio `("I"_"max" - "I"_"min")/("I"_"max" + "I"_"min")` will be ______
In Young's double-slit experiment, in an interference pattern, a second minimum is observed exactly in front of one slit. The distance between the two coherent sources is 'd' and the distance between source and screen is 'D'. The wavelength of the light source used is ______
A thin transparent sheet is placed in front of a slit in Young's double slit experiment. The fringe width will ____________.
In Young's experiment for the interference of light, the separation between the silts is d and the distance of the screen from the slits is D. If D is increased by 0.6% and d is decreased by 0.2%, then for the light of a given wavelength, which one of the following is true?
"The fringe width ____________."
In Young's experiment, the distance between the slits is doubled and the distance between the slit and screen is reduced to half, then the fringe width ____________.
In a double slit experiment, the two slits are 2 mm apart and the screen is placed 1 m away. A monochromatic light of wavelength 500 nm is used. What will be the width of each slit for obtaining ten maxima of double slit within the central maxima of single slit pattern?
In a biprism experiment, D = 1 m, `lambda` = 6000 Å. When a convex lens is interposed between the biprism ru1d the eyepiece, then the distance between the images of the slits given by the Jens at two positions are 1.5 mm and 6.0 mm. The fringe width will be ______.
In Young's double slit experiment fifth dark fringe is formed opposite to one of the slits. If D is the distance between the slits and the screen and d is the separation between the slits, then the wavelength of light used is ______.
In interference experiment, intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at (sin30° = cos60° = 0.5, `lambda` = wavelength of light, d = slit width) ____________.
In a biprism experiment, red light of wavelength 6500 Å was used. It was then replaced by green light of wavelength 5200 Å. The value of n for which (n + 1)th green bright band would coincide with nth red bright band for the same setting is ______.
If two light waves reaching a point produce destructive interference, then the condition of phase difference is ______
The graph shows the variation of fringe width (β) versus distance of the screen from the plane of the slits (D) in Young's double-slit experiment Keeping other parameters the same. The wavelength of light used can be calculated as d = distance between the slits ______

In Young's double-slit experiment, the distance between the slits is 3 mm and the slits are 2 m away from the screen. Two interference patterns can be obtained on the screen due to light of wavelength 480 nm and 600 run respectively. The separation on the screen between the 5th order bright fringes on the two interference patterns is ______
In an interference experiment, the intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at ____________.
(cos 60° = 0.5, `lambda` = wavelength of light, d = slit width)
Two coherent sources of intensities I1 and I2 produce an interference pattern on the screen. The maximum intensity in the interference pattern is ______
What is meant by Constructive interference?
White light is passed through a double slit and interference is observed on a screen 1.5 m away. The separation between the slits is 0.3 mm. The first violet and red fringes are formed 2.0 mm and 3.5 mm away from the central white fringes. The difference in wavelengths of red and violet light is ______ nm.
In a double-slit experiment, the optical path difference between the waves coming from two coherent sources at a point P on one side of the central bright is 7.5 µm and that at a point Q on the other side of the central bright fringe and 1.8 µm. How many bright and dark fringes are observed between points P and Q if the wavelength of light used is 600 nm?
