Advertisements
Advertisements
प्रश्न
A double-slit arrangement produces interference fringes for sodium light (λ = 589 nm) that are 0.20° apart. What is the angular fringe separation if the entire arrangement is immersed in water (n = 1.33)?
उत्तर
Given: θ1 = 0.20°, nw = 1.33
In the first approximation,
D sin θ1 = y1 and D sin θ2 = y2
`therefore (sin theta_2)/(sin theta_1) = "y"_2/"y"_1` ...(1)
Now, `y prop (lambdaD)/d`
For given d and D,
y ∝ λ
∴ `y_2/y_1 = lambda_2/lambda_1` ...(2)
Now, `n_w = lambda_1/lambda_2` ...(3)
From Eqs. (1), (2) and (3), we get
`(sin theta_2)/(sin theta_1) = lambda_2/lambda_1 = 1/n_w`
∴ `sin theta_2 = sin theta_1/n_w`
`sin theta_2 = (sin 0.2)/1.33`
`sin theta_2 = 0.0035/1.33`
sinθ2 = 0.0026
θ2 = sin−1 0.0026
θ2 = 9'
θ2 = 0.15°
This is the required angular fringe separation.
संबंधित प्रश्न
Laser light of wavelength 630 nm is incident on a pair of slits which are separated by 1.8 mm. If the screen is kept 80 cm away from the two slits, calculate:
1) fringe separation i.e. fringe width.
2) distance of 10th bright fringe from the centre of the interference pattern
The intensity at the central maximum (O) in a Young’s double slit experimental set-up shown in the figure is IO. If the distance OP equals one-third of the fringe width of the pattern, show that the intensity at point P, would equal `(I_0)/4`.

In Young’s double slit experiment, the slits are separated by 0.5 mm and screen is placed 1.0 m away from the slit. It is found that the 5th bright fringe is at a distance of 4.13 mm from the 2nd dark fringe. Find the wavelength of light used.
Answer the following question.
Describe any two characteristic features which distinguish between interference and diffraction phenomena. Derive the expression for the intensity at a point of the interference pattern in Young's double-slit experiment.
Answer in brief:
What is meant by coherent sources?
What is interference of light?
Obtain the relation between phase difference and path difference.
How does wavefront division provide coherent sources?
Obtain the equation for resultant intensity due to interference of light.
The distance between the first and ninth bright fringes formed in a biprism experiment is ______.
(`lambda` = 6000 A, D = 1.0 m, d = 1.2 mm)
Two identical light waves having phase difference 'Φ' propagate in same direction. When they superpose, the intensity of the resultant wave is proportional to ______.
In Young's experiment for the interference of light, the separation between the silts is d and the distance of the screen from the slits is D. If D is increased by 0.6% and d is decreased by 0.2%, then for the light of a given wavelength, which one of the following is true?
"The fringe width ____________."
In a biprism experiment, D = 1 m, `lambda` = 6000 Å. When a convex lens is interposed between the biprism ru1d the eyepiece, then the distance between the images of the slits given by the Jens at two positions are 1.5 mm and 6.0 mm. The fringe width will be ______.
A thin mica sheet of thickness 4 x 10-6 m and refractive index 1.5 is introduced in the path of the first wave. The wavelength of the wave used is 5000 A. The central bright maximum will shift ______.
In Young's double slit experiment, the two slits act as coherent sources of equal amplitude A and wavelength `lambda`. In another experiment with the same set up the two slits are of equal amplitude A and wavelength `lambda`. but are incoherent. The ratio of the intensity of light at the mid-point of the screen in the first case to that in the second case is ____________.
The phenomenon of interference is based on ______.
In the Young's double slit experiment, if the phase difference between the two waves interfering at a point is `phi`, the intensity at that point is proportional to ____________.
Two identical light sources s1 and s2 emit light of same wavelength `lambda`. These light rays will exhibit interference if their ______.
In the biprism experiment, the fringe width is 0.4 mm. What is the distance between the 4th dark band and the 6th bright band on the same side?
In a biprism experiment, monochromatic light of wavelength (λ) is used. The distance between two coherent sources is kept constant. If the distance between slit and eyepiece (D) is varied as D1, D2, D3, and D4, the corresponding measured fringe widths are z1, z2, z3, and z4 then ______
In Young's double-slit experiment, if the two sources of light are very wide, then ______.
Two waves with same amplitude and frequency superpose at a point. The ratio of resultant intensities when they arrive in phase to that when they arrive 90° out of phase is ______.
`[cos pi/2=0]`
A double slit experiment is immersed in water of refractive index 1.33. The slit separation is 1 mm, distance between slit and screen is 1.33 m. The slits are illuminated by a light of wavelength 6300 Å. The fringe width is ______.
In an interference experiment, the intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at ____________.
(cos 60° = 0.5, `lambda` = wavelength of light, d = slit width)
How will the interference pattern of Young's double slit change if one of the two slits is covered by a paper which transmits only half of the light intensity?
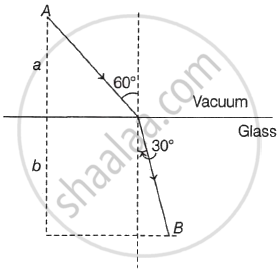
A ray of light AO in vacuum is incident on a glass slab at angle 60° and refracted at angle 30° along OB as shown in the figure. The optical path length of light ray from A to B is ______.
With a neat labelled ray diagram explain the use of Fresnel's biprism to obtain two coherent sources.
In biprism experiment, the distance of 20th bright band from the central bright band is 1.2 cm. Without changing the experimental set-up, the distance of 30th bright band from the central bright band will be ______.
