Advertisements
Advertisements
Question
Describe geometry of the Young’s double slit experiment with the help of a ray diagram. What is fringe width? Obtain an expression of it. Write the conditions for constructive as well as destructive interference.
Solution
i. Let S1 and S2 be the two coherent monochromatic sources that are separated by short distance d. They emit light waves of wavelength λ.
ii. Let D = horizontal distance between screen and source.
iii. Draw S1M and S2N ⊥ AB
OP = perpendicular bisector of the slit.
Since S1P = S2P, the path difference between waves reaching P from S1 and S2 is zero, therefore there is a bright point at P.
iv. Consider a point Q on the screen which is at a distance y from the central point P on the screen. Light waves from S1 and S2 reach at Q simultaneously by covering paths S1Q and S2Q, where they superimpose. 
Derivation:
In Δ S1MQ, (S1Q)2 = (S1M)2 + (MQ)2
`("S"_1"Q")^2 = "D"^2 + ["y" - "d"/2]^2` ....(1)
In `Δ "S"_2"NQ", ("S"_2"Q")^2 = ("S"_2"N")^2 + ("NQ")^2`
∴ `("S"_2"Q")^2 = "D"^2 + ["y" + "d"/2]^2` ....(2)
Subtract equation (1) from (2),
`("S"_2"Q")^2 - ("S"_1"Q")^2 = ["D"^2 + ("y" + "d"/2)^2] - ["D"^2 + ("y" - "d"/2)^2]`
= `"D"^2 + ("y" + "d"/2)^2 - "D"^2 - ("y" - "d"/2)^2`
= `("y" + "d"/2)^2 - ("y" - "d"/2)^2`
= `("y"^2 + "d"^2/4 + "yd") - ("y"^2 + "d"^2/4 - "yd")`
= `"y"^2 + "d"^2/4 + "yd" - "y"^2 - "d"^2/4 + "yd"("S"_2"Q")^2 - ("S"_1"Q")^2`
= 2yd
∴ `("S"_2"Q" + "S"_1"Q")("S"_2"Q" - "S"_1"Q")` = 2yd
∴ `"S"_2"Q" - "S"_1"Q" = (2"yd")/("S"_2"Q" + "S"_1"Q")` ....(3)
If y << D and d << D then, S1Q ≈ S2Q ≈ D
S2Q + S1Q = 2D
∴ Equation (3) becomes,
`"S"_2"Q" - "S"_1"Q" = (2"yd")/(2"D")`
∴ `"S"_2"Q" - "S"_1"Q" = "yd"/"D"`
∴ Δl = `"yd"/"D"` ....(4)
Equation (4) gives the path difference of two interfering light waves. Point Q will be bright if,
Δl = nλ = 2n`lambda/2`
where n = 0, 1, 2,….
∴ `("y"_"n""d")/"D" = "n"λ = 2"n"lambda/2` ........….[From equation (4)]
∴ `"y"_"n" = "n"(lambda"D")/"d"` ….(5)
Equation (5) represents the distance of the nth bright fringe from the central bright fringe.
Point Q will be a dark point if,
`Deltal = (2"n" - 1)lambda/2`
where n = 1, 2, 3,……
∴ `("y"_"n"^'"d")/"D" = (2"n" - 1)lambda/2`
∴ `"y"_"n"^' = (2"n" - 1)(lambda"D")/(2"d") = ("n" - 1/2) (lambda"D")/"d"` .........(6)
Equation (6) represents the distance of nth dark fringe from the central maximum.
Fringe width:
The distance between any two successive dark or any two successive bright fringes is equal. This is called the fringe width and is given by, Fringe width = W = Δy = `"y"_("n" + 1) - "y"_"n" = "y"_"n + 1"^' - "y"_"n"^'`
W = `λ"D"/"d"`
Thus, both dark and bright fringes are equidistant and have equal widths.
Conditions for constructive and destructive interference:
The phase difference between the two waves reaching P, from `"S"_1` and `"S"_2` is given by,
`Deltaphi = "y""d"/"D"((2pi)/lambda)` ..........`(∵ Deltal = "yd"/"D")`
The condition for constructive interference in terms of phase difference is given by,
ΔΦ = n2π, where, n = 0, ±1 ±2
∴ The condition for destructive interference in terms of phase difference is given by
`Deltaphi = ("n" - 1/2)2pi,` where, n = ±1, ±2
APPEARS IN
RELATED QUESTIONS
A long narrow horizontal slit is paced 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 m away from the slit. Find the fringe-width if the light used has a wavelength of 700 nm.
The intensity at the central maximum (O) in a Young’s double slit experimental set-up shown in the figure is IO. If the distance OP equals one-third of the fringe width of the pattern, show that the intensity at point P, would equal `(I_0)/4`.

In Young’s double slit experiment, the slits are separated by 0.5 mm and screen is placed 1.0 m away from the slit. It is found that the 5th bright fringe is at a distance of 4.13 mm from the 2nd dark fringe. Find the wavelength of light used.
What are the two methods for obtaining coherent sources in the laboratory?
A double-slit arrangement produces interference fringes for sodium light (λ = 589 nm) that are 0.20° apart. What is the angular fringe separation if the entire arrangement is immersed in water (n = 1.33)?
What is interference?
One of Young’s double slits is covered with a glass plate as shown in figure. The position of central maximum will,
What is interference of light?
How do source and images behave as coherent sources?
Explain Young’s double-slit experimental setup and obtain the equation for path difference.
Discuss the interference in thin films and obtain the equations for constructive and destructive interference for transmitted and reflected light.
In Young’s double slit experiment, the slits are 2 mm apart and are illuminated with a mixture of two wavelength λ0 = 750 nm and λ = 900 nm. What is the minimum distance from the common central bright fringe on a screen 2 m from the slits where a bright fringe from one interference pattern coincides with a bright fringe from the other?
The interference pattern is obtained with two coherent light sources of intensity ratio n. In the interference pattern, the ratio `("I"_"max" - "I"_"min")/("I"_"max" + "I"_"min")` will be ______
The light waves from two independent monochromatic light sources are given by, y1 = 2 sin ωt and y2 = 3 cos ωt. Then the correct statement is ____________.
In Young's experiment, the distance between the slits is doubled and the distance between the slit and screen is reduced to half, then the fringe width ____________.
If the two slits in Young's double slit experiment have width ratio 9 : 1, the ratio of maximum to minimum intensity in the interference pattern is ______.
If two waves represented by `"y"_1 = 3 "sin" omega "t"` and `"y"_2 = 5 "sin" (omega "t" + pi/3)` interfere at a point, then the amplitude of the resulting wave will be about ____________.
In the biprism experiment, the fringe width is 0.4 mm. What is the distance between the 4th dark band and the 6th bright band on the same side?
Waves from two coherent sources of light having an intensity ratio I1 : I2 equal to 'x' interfere. Then in the interference pattern obtained on the screen, the value of (Imax - Imin)/(Imax + Imin) is ______
Two waves with same amplitude and frequency superpose at a point. The ratio of resultant intensities when they arrive in phase to that when they arrive 90° out of phase is ______.
`[cos pi/2=0]`
In Young's double-slit experiment, the distance between the slits is 3 mm and the slits are 2 m away from the screen. Two interference patterns can be obtained on the screen due to light of wavelength 480 nm and 600 run respectively. The separation on the screen between the 5th order bright fringes on the two interference patterns is ______
In Young's double-slit experiment, the distance between the slits is 3 mm and the slits are 2 m away from the screen. Two interference patterns can be obtained on the screen due to light of wavelength 480 nm and 600 run respectively. The separation on the screen between the 5th order bright fringes on the two interference patterns is ______
In an interference experiment, the intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at ____________.
(cos 60° = 0.5, `lambda` = wavelength of light, d = slit width)
Interference fringes are produced on a screen by using two light sources of intensities I and 9I. The phase difference between the beams is `pi/2` at point P and π at point Q on the screen. The difference between the resultant intensities at point P and Q is ______.
Two coherent sources P and Q produce interference at point A on the screen where there is a dark band which is formed between 4th bright band and 5th bright band. Wavelength of light used is 6000 Å. The path difference between PA and QA is ______.
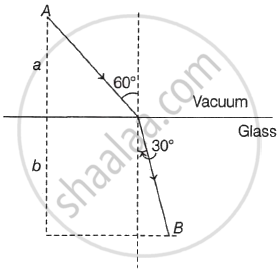
A ray of light AO in vacuum is incident on a glass slab at angle 60° and refracted at angle 30° along OB as shown in the figure. The optical path length of light ray from A to B is ______.
In biprism experiment, the distance of 20th bright band from the central bright band is 1.2 cm. Without changing the experimental set-up, the distance of 30th bright band from the central bright band will be ______.
