Advertisements
Advertisements
Question
Explain Young’s double-slit experimental setup and obtain the equation for path difference.
Solution

Young’s double-slit experiment
- Wavefronts from S1 and S2 spread out and overlapping takes place to the right side of the double slit.
- When a screen is placed at a distance of about 1 meter from the slits, alternately bright and dark fringes which are equally spaced appear on the screen. These are called interference fringes or bands.
Equation for path difference: - Let d be the distance between the double slits S1 and S2 which act as coherent sources of wavelength λ.
- A screen is placed parallel to the double-slit at a distance D from it. The mid-point of S1 and S2 is C and the mid-point of the screen O is equidistant from S1 and S2. P is any point at a distance y from O.
- The waves from S1 and S2 meet at P either in-phase or out-of-phase depending upon the path difference between the two waves.
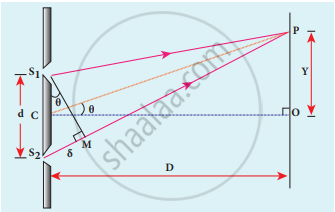
Young’s double-slit experimental setupδ = S2P – S1P
δ = S2P – MP = S2M -
The angular position of the point P from C is θ. ∠ OCP = θ.
- From the geometry, the angles ∠ OCP and ∠ S2S1M are equal.
∠ OCP = ∠ S2S1M = θ.
In right-angle triangle ∆ S1S2M, the path difference,
S2M = d sin θ
δ = d sin θ
If the angle θ is small, sin θ »tan θ θ
From the right angle triangle ∆ OCP,
tan θ = `"y"/"D"`
The path difference, δ = `"dy"/"d"`
APPEARS IN
RELATED QUESTIONS
Write the important characteristic features by which the interference can be distinguished from the observed diffraction pattern.
When a drop of oil is spread on a water surface, it displays beautiful colours in daylight because of ______________ .
Four light waves are represented by
(i) \[y = a_1 \sin \omega t\]
(ii) \[y = a_2 \sin \left( \omega t + \epsilon \right)\]
(iii) \[y = a_1 \sin 2\omega t\]
(iv) \[y = a_2 \sin 2\left( \omega t + \epsilon \right).\]
Interference fringes may be observed due to superposition of
(a) (i) and (ii)
(b) (i) and (iii)
(c) (ii) and (iv)
(d) (iii) and (iv)
A long narrow horizontal slit is paced 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 m away from the slit. If the mirror reflects only 64% of the light energy falling on it, what will be the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen?
In Young’s double slit experiment, the slits are separated by 0.5 mm and screen is placed 1.0 m away from the slit. It is found that the 5th bright fringe is at a distance of 4.13 mm from the 2nd dark fringe. Find the wavelength of light used.
Answer in brief:
In Young's double-slit experiment what will we observe on the screen when white light is incident on the slits but one slit is covered with a red filter and the other with a violet filter? Give reasons for your answer.
What is phase of a wave?
What is a bandwidth of interference pattern?
Discuss the interference in thin films and obtain the equations for constructive and destructive interference for transmitted and reflected light.
In Young’s double-slit experiment, 62 fringes are seen in the visible region for sodium light of wavelength 5893 Å. If violet light of wavelength 4359 Å is used in place of sodium light, then what is the number of fringes seen?
In Young's double slit experiment green light is incident on the two slits. The interference pattern is observed on a screen. Which one of the following changes would cause the observed fringes to be more closely spaced?
Band width for red light of wavelength 6600 Å is 0.42 mm. If red Light is replaced by blue light of wavelength 4400 Å, then the change m bandwidth will be ____________.
In Young's experiment for the interference of light, the separation between the silts is d and the distance of the screen from the slits is D. If D is increased by 0.6% and d is decreased by 0.2%, then for the light of a given wavelength, which one of the following is true?
"The fringe width ____________."
In a double slit experiment, the two slits are 2 mm apart and the screen is placed 1 m away. A monochromatic light of wavelength 500 nm is used. What will be the width of each slit for obtaining ten maxima of double slit within the central maxima of single slit pattern?
The phenomenon of interference is based on ______.
In Young's double-slit experiment, the distance between the slits is 3 mm and the slits are 2 m away from the screen. Two interference patterns can be obtained on the screen due to light of wavelength 480 nm and 600 run respectively. The separation on the screen between the 5th order bright fringes on the two interference patterns is ______
In an interference experiment, the intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at ____________.
(cos 60° = 0.5, `lambda` = wavelength of light, d = slit width)
The path difference between two interference light waves meeting at a point on the screen is `(87/2)lambda`. The band obtained at that point is ______.
In a double-slit experiment, the optical path difference between the waves coming from two coherent sources at a point P on one side of the central bright is 7.5 µm and that at a point Q on the other side of the central bright fringe and 1.8 µm. How many bright and dark fringes are observed between points P and Q if the wavelength of light used is 600 nm?
With a neat labelled ray diagram explain the use of Fresnel's biprism to obtain two coherent sources.
