Advertisements
Advertisements
प्रश्न
Explain Young’s double-slit experimental setup and obtain the equation for path difference.
उत्तर

Young’s double-slit experiment
- Wavefronts from S1 and S2 spread out and overlapping takes place to the right side of the double slit.
- When a screen is placed at a distance of about 1 meter from the slits, alternately bright and dark fringes which are equally spaced appear on the screen. These are called interference fringes or bands.
Equation for path difference: - Let d be the distance between the double slits S1 and S2 which act as coherent sources of wavelength λ.
- A screen is placed parallel to the double-slit at a distance D from it. The mid-point of S1 and S2 is C and the mid-point of the screen O is equidistant from S1 and S2. P is any point at a distance y from O.
- The waves from S1 and S2 meet at P either in-phase or out-of-phase depending upon the path difference between the two waves.
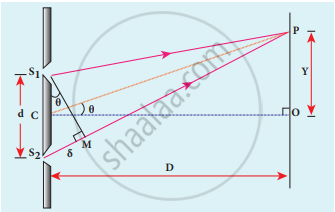
Young’s double-slit experimental setupδ = S2P – S1P
δ = S2P – MP = S2M -
The angular position of the point P from C is θ. ∠ OCP = θ.
- From the geometry, the angles ∠ OCP and ∠ S2S1M are equal.
∠ OCP = ∠ S2S1M = θ.
In right-angle triangle ∆ S1S2M, the path difference,
S2M = d sin θ
δ = d sin θ
If the angle θ is small, sin θ »tan θ θ
From the right angle triangle ∆ OCP,
tan θ = `"y"/"D"`
The path difference, δ = `"dy"/"d"`
APPEARS IN
संबंधित प्रश्न
A long narrow horizontal slit is paced 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 m away from the slit. Find the fringe-width if the light used has a wavelength of 700 nm.
The intensity at the central maximum (O) in a Young’s double slit experimental set-up shown in the figure is IO. If the distance OP equals one-third of the fringe width of the pattern, show that the intensity at point P, would equal `(I_0)/4`.

Why are multiple colours observed over a thin film of oil floating on water? Explain with the help of a diagram.
Two coherent sources whose intensity ratio is 25:1 produce interference fringes. Calculate the ratio of amplitudes of light waves coming from them.
One of Young’s double slits is covered with a glass plate as shown in figure. The position of central maximum will,
Obtain the relation between phase difference and path difference.
How does wavefront division provide coherent sources?
How do source and images behave as coherent sources?
Obtain the equation for resultant intensity due to interference of light.
On a rainy day, a small oil film on water shows brilliant colours. This is due to ____________.
The distance between the first and ninth bright fringes formed in a biprism experiment is ______.
(`lambda` = 6000 A, D = 1.0 m, d = 1.2 mm)
In Young's experiment for the interference of light, the separation between the silts is d and the distance of the screen from the slits is D. If D is increased by 0.6% and d is decreased by 0.2%, then for the light of a given wavelength, which one of the following is true?
"The fringe width ____________."
The phenomenon of interference is based on ______.
In a biprism experiment, red light of wavelength 6500 Å was used. It was then replaced by green light of wavelength 5200 Å. The value of n for which (n + 1)th green bright band would coincide with nth red bright band for the same setting is ______.
Two coherent light sources of intensity ratio 'n' are employed in an interference experiment. The ratio of the intensities of the maxima and minima in the interference pattern is (I1 > I2).
In a biprism experiment, the slit separation is 1 mm. Using monochromatic light of wavelength 5000 Å, an interference pattern is obtained on the screen. Where should the screen be moved? so that the change in fringe width is 12.5 x 105 m?
In the biprism experiment, a source of monochromatic light is used for a certain distance between slit and eyepiece. When the distance between two virtual sources is changed from dA to dB, then the fringe width is changed from ZA to ZB. The ratio ZA to ZB is ______
Two coherent sources of intensities I1 and I2 produce an interference pattern on the screen. The maximum intensity in the interference pattern is ______
If we have two coherent sources S1 and S2 vibrating in phase, then for an arbitrary point P constructive interference is observed whenever the path difference is ______.
How will the interference pattern of Young's double slit change if one of the two slits is covered by a paper which transmits only half of the light intensity?
