Advertisements
Advertisements
प्रश्न
Explain Young’s double-slit experimental setup and obtain the equation for path difference.
उत्तर

Young’s double-slit experiment
- Wavefronts from S1 and S2 spread out and overlapping takes place to the right side of the double slit.
- When a screen is placed at a distance of about 1 meter from the slits, alternately bright and dark fringes which are equally spaced appear on the screen. These are called interference fringes or bands.
Equation for path difference: - Let d be the distance between the double slits S1 and S2 which act as coherent sources of wavelength λ.
- A screen is placed parallel to the double-slit at a distance D from it. The mid-point of S1 and S2 is C and the mid-point of the screen O is equidistant from S1 and S2. P is any point at a distance y from O.
- The waves from S1 and S2 meet at P either in-phase or out-of-phase depending upon the path difference between the two waves.
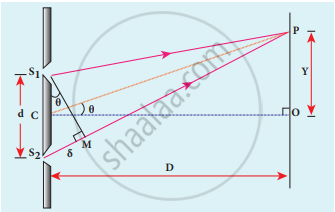
Young’s double-slit experimental setupδ = S2P – S1P
δ = S2P – MP = S2M -
The angular position of the point P from C is θ. ∠ OCP = θ.
- From the geometry, the angles ∠ OCP and ∠ S2S1M are equal.
∠ OCP = ∠ S2S1M = θ.
In right-angle triangle ∆ S1S2M, the path difference,
S2M = d sin θ
δ = d sin θ
If the angle θ is small, sin θ »tan θ θ
From the right angle triangle ∆ OCP,
tan θ = `"y"/"D"`
The path difference, δ = `"dy"/"d"`
APPEARS IN
संबंधित प्रश्न
Laser light of wavelength 630 nm is incident on a pair of slits which are separated by 1.8 mm. If the screen is kept 80 cm away from the two slits, calculate:
1) fringe separation i.e. fringe width.
2) distance of 10th bright fringe from the centre of the interference pattern
How does the angular separation between fringes in single-slit diffraction experiment change when the distance of separation between the slit screens is doubled?
Four light waves are represented by
(i) \[y = a_1 \sin \omega t\]
(ii) \[y = a_2 \sin \left( \omega t + \epsilon \right)\]
(iii) \[y = a_1 \sin 2\omega t\]
(iv) \[y = a_2 \sin 2\left( \omega t + \epsilon \right).\]
Interference fringes may be observed due to superposition of
(a) (i) and (ii)
(b) (i) and (iii)
(c) (ii) and (iv)
(d) (iii) and (iv)
In a Young’s double-slit experiment, the slit separation is doubled. To maintain the same fringe spacing on the screen, the screen-to-slit distance D must be changed to ______.
What is interference of light?
How does wavefront division provide coherent sources?
What is a bandwidth of interference pattern?
The interference pattern is obtained with two coherent light sources of intensity ratio n. In the interference pattern, the ratio `("I"_"max" - "I"_"min")/("I"_"max" + "I"_"min")` will be ______
In Young's double-slit experiment, if the width of the 2nd bright fringe is 4 x 10-2 cm, then the width of the 4th bright fringe will be ______ cm.
In Young's double-slit experiment, in an interference pattern, a second minimum is observed exactly in front of one slit. The distance between the two coherent sources is 'd' and the distance between source and screen is 'D'. The wavelength of the light source used is ______
Two identical light waves having phase difference 'Φ' propagate in same direction. When they superpose, the intensity of the resultant wave is proportional to ______.
In Young's double slit experiment fifth dark fringe is formed opposite to one of the slits. If D is the distance between the slits and the screen and d is the separation between the slits, then the wavelength of light used is ______.
In interference experiment, intensity at a point is `(1/4)^"th"` of the maximum intensity. The angular position of this point is at (sin30° = cos60° = 0.5, `lambda` = wavelength of light, d = slit width) ____________.
`phi "and" phi_2 (phi_1 > phi_2)` are the work functions of metals A and B. When light of same wavelength is incident on A and B, the fastest emitted electrons from A are ____________ those emitted from B.
In the biprism experiment, the fringe width is 0.4 mm. What is the distance between the 4th dark band and the 6th bright band on the same side?
Two waves with same amplitude and frequency superpose at a point. The ratio of resultant intensities when they arrive in phase to that when they arrive 90° out of phase is ______.
`[cos pi/2=0]`
How will the interference pattern of Young's double slit change if one of the two slits is covered by a paper which transmits only half of the light intensity?
White light is passed through a double slit and interference is observed on a screen 1.5 m away. The separation between the slits is 0.3 mm. The first violet and red fringes are formed 2.0 mm and 3.5 mm away from the central white fringes. The difference in wavelengths of red and violet light is ______ nm.
Describe Young's double-slit interference experiment.
With a neat labelled ray diagram explain the use of Fresnel's biprism to obtain two coherent sources.
