Advertisements
Advertisements
प्रश्न
Two cubes, each of volume 512 cm3 are joined end to end. Find the surface area of the resulting cuboid.
उत्तर
\[\text { Two cubes each of volume 512 } {cm}^3\text { are joined end to end . }\]
\[\text { Now, volume of a cube = (side ) }^3 \]
\[ \Rightarrow 512 = \text { (side ) }^3 \]
\[ \Rightarrow\text { Side of the cube = }\sqrt[3]{512} = 8 cm \]
\[\text { If the cubes area joined side by side, then the length of the resulting cuboid is 2 } + \times 8 cm = 16 cm . \]
\[\text { Breadth = 8 cm } \]
\[\text { Height = 8 cm }\]
\[ \therefore \text { Surface area of the cuboid = 2 } \times\text { (length }\times \text { breadth + breadth } \times \text{ height + length } \times \text { height) }\]
\[ = 2 \times (16 \times 8 + 8 \times 8 + 16 \times 8)\]
\[ = 2 \times (128 + 64 + 128)\]
\[ = 640 {cm}^2\]
APPEARS IN
संबंधित प्रश्न
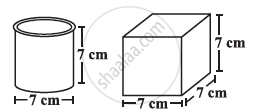
Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?
A cube A has side thrice as long as that of cube B. What is the ratio of the volume of cube A to that of cube B?
Find the volume in cubic decimetre of the cube whose side is 1.5 m.
Find the volume of a cube whose surface area is 150 m2 .
Find the length of 13.2 kg of copper wire of diameter 4 mm, when 1 cubic cm of copper weighs 8.4 gm.
Three equal cubes are placed adjacently in a row. Find the ratio of the total surfaced area of the resulting cuboid to that of the sum of the total surface areas of the three cubes.
The ratio between the lengths of the edges of two cubes is in the ratio 3: 2. Find the ratio between their:
(i) total surface area
(ii) volume.
A solid cube of side 12 cm is cut into 8 identical cubes. What will be the side of the new cube? Also, find the ratio between the surface area of the original cube and the total surface area of all the small cubes formed.
Find the volume of a cube whose diagonals is `sqrt(48)"cm"`.
The areas of any two faces of a cube are equal.
