Advertisements
Advertisements
प्रश्न
Two customers are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any one day as on another. What is the probability that both will visit the shop on different days?
उत्तर
Total no. of days to visit the shop = 6 {Mon to Sat}
otal no. possible outcomes = 6 × 6 = 36
i.e. two customers can visit the shop in 36 ways
E⟶ event of visiting shop on the same day.
`barE`⟶ event of visiting shop on the different days.
In above bit, we calculated P(E) as 1/6
We know that, P(E) + P(`barE`) = 1
P(`barE` ) = 1 – P(E)
= 1 − 1/6
=5/6
संबंधित प्रश्न
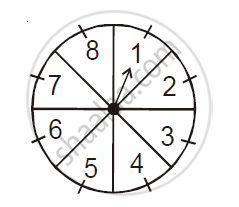
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see the given figure), and these are equally likely outcomes. What is the probability that it will point at
- 8?
- an odd number?
- a number greater than 2?
- a number less than 9?
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting a spade.
A card is drawn at random from a pack of 52 cards. Find the probability that card drawn is jack
A black die and a white die are thrown at the same time. Write all the possible outcomes. What is the probability? that the sum of the two numbers that turn up is 8?
A black die and a white die are thrown at the same time. Write all the possible outcomes. What is the probability? of obtaining the same number on both dice?
The king, queen and jack of clubs are removed from a deck of 52 playing cards and the remaining cards are shuffled. A card is drawn from the remaining cards. Find the
probability of getting a card of queen
From a well-shuffled deck of 52 playing-cards, one card is drawn. Find the probability that the card drawn will be a face card of red colour.
There are six cards in a box, each bearing a number from 0 to 5. Find the probability of the following event, that a card drawn show, a number is greater than 5.
Fill in the blank:
For any event E, P(E) + P (not E) = ........ .
All the jacks, queens and kings are removed from a deck of 52 playing cards. The remaining cards are well shuffled and then one card is drawn at random. Giving ace a value 1 similar value for other cards, find the probability that the card has a value 7
