Advertisements
Advertisements
प्रश्न
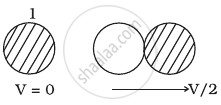
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in figure.
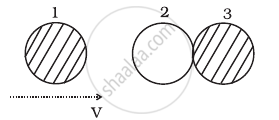
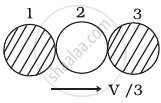
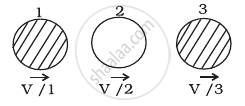
If the collision is elastic, which of the following (Figure) is a possible result after collision?
विकल्प
उत्तर
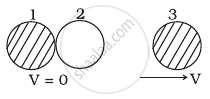
Explanation:
In a collision, if the motion of colliding particles before and after the collision is along the same line, the collision is said to be head-on or one-dimensional.
When two bodies of equal masses collide elastically, their velocities are interchanged.
Kinetic energy and linear momentum remain conserved Total kinetic energy of the system before the collision
= `1/2 mv^2 + 0 = 1/2 mv^2`
In (a), kinetic energy of the system after the collision.
`k_1 = 1/2 (2m) (v/2)^2 = 1/4 mv^2`
Hence this option is incorrect.
In (b), kinetic energy of the system after the collision.
`k_2 = 1/2 (m) (v)^2 = 1/2 mv^2`
Hence this option will be correct.
In (c), kinetic energy of the system after the collision.
`k_3 = 1/2 (3m) (v/3)^2 = 1/6 mv^2`
Hence this option is incorrect.
In (d), kinetic energy of the system after the collision.
`k_4 = 1/2 mv^2 + 1/2 m (v/2)^2 + 1/2 m(v/3)^2 = 49/72 mv^2`
We see that kinetic energy is conserved only in (b).
APPEARS IN
संबंधित प्रश्न
In an inelastic collision of two bodies, the quantities which do not change after the collision are the ______ of the system of two bodies.
A molecule in a gas container hits a horizontal wall with speed 200 m s–1 and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?
Answer the following question.
A bullet of mass m1 travelling with a velocity u strikes a stationary wooden block of mass m2 and gets embedded into it. Determine the expression for loss in the kinetic energy of the system. Is this violating the principle of conservation of energy? If not, how can you account for this loss?
Define the following:
Coefficient of restitution
A block of mass 'm' moving on a frictionless surface at speed 'v' collides elastically with a block of same mass, initially at rest. Now the first block moves at an angle 'θ' with its initial direction and has speed 'v1'. The speed of the second block after collision is ______.
A ball of mass 0.1 kg makes an elastic head-on collision with a ball of unknown mass, initially at rest. If the 0 .1 kg ball rebounds at one-third of its original speed, the mass of the other ball is ______.
In inelastic collision, ____________.
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
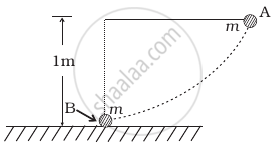
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
An insect moves with a constant velocity v from one corner of a room to other corner which is opposite of the first corner along the largest diagonal of room. If the insect can not fly and dimensions of room is a × a × a, then the minimum time in which the insect can move is `"a"/"v"`. times the square root of a number n, then n is equal to ______.
Three identical blocks A, B and C are placed on horizontal frictionless surface. The blocks A and C are at rest. But A is approaching towards B with a speed 10 m/s. The coefficient of restitution for all collision is 0.5. The speed of the block C just after the collision is ______.