Advertisements
Advertisements
प्रश्न
Two tiny spheres carrying charges 1.5 μC and 2.5 μC are located 30 cm apart. Find the potential and electric field:
(a) at the mid-point of the line joining the two charges, and
(b) at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.
Advertisements
उत्तर
Two charges placed at points A and B are represented in the given figure. O is the mid-point of the line joining the two charges.
Magnitude of charge located at A, q1 = 1.5 μC
Magnitude of charge located at B, q2 = 2.5 μC
Distance between the two charges, d = 30 cm = 0.3 m
(a) Let V1 and E1 are the electric potentials and electric field respectively at O.
V1 = Potential due to charge at A + Potential due to charge at B
`"V"_1 = "q"_1/(4piin_0("d"/2)) + "q"_2/(4piin_0("d"/2)) = 1/(4piin_0("d"/2))("q"_1 + "q"_2)`
Where,
∈0 = Permittivity of free space
`1/(4piin_0) = 9 xx 10^9 "N C"^2 "m"^-2`
∴ `"V"_1 = (9 xx 10^9 xx 10^-6)/((0.30/2))(2.5 + 1.5)`
= `2.4 xx 10^5 "V"`
E1 = Electric field due to q2 − Electric field due to q1
= `"q"_2/(4piin_0("d"/2)^2) - "q"_1/(4piin_0("d"/2)^2)`
= `(9 xx 10^9)/((0.30/2)^2) xx 10^6 xx (2.5 - 1.5)`
= `4 xx 10^5 "V m"^-1`
Therefore, the potential at mid-point is 2.4 × 105 V and the electric field at mid-point is 4 × 105 V m−1. The field is directed from the larger charge to the smaller charge.
(b) Consider a point Z such that normal distance OZ = 10 cm = 0.1 m, as shown in the following figure.
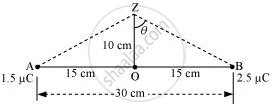
V2 and E2 are the electric potential and electric field respectively at Z.
It can be observed from the figure that distance,
`"BZ" = "AZ" = sqrt((0.1)^2 + (0.15)^2)` = 0.18 m
V2 = Electric potential due to A + Electric Potential due to B
= `"q"_1/(4piin_0("AZ")) + "q"_2/(4piin_0("BZ"))`
= `(9 xx 10^9 xx 10^-6)/0.18(1.5 + 2.5)`
Electric field due to q at Z,
`"E"_"A" = "q"_1/(4piin_0("AZ")^2)`
= `(9 xx 10^9 xx 1.5 xx 10^-6)/(0.18)^2`
= `0.416 xx 10^6 "V"/"m"`
Electric field due to q2 at Z,
`E_"B" = "q"_2/(4piin_0("BZ")^2)`
= `(9 xx 10^9 xx 2.5 xx 10^-6)/(0.18)^2`
= `0.69 xx 10^6 "V m"^-1`
The resultant field intensity at Z,
`"E" = sqrt("E"_"A"^2 + "E"_"B"^2 + 2"E"_"A""E"_"B"cos 2 theta)`
Where, 2θ is the angle, ∠AZB
From the figure, we obtain
`cos theta = 0.10/0.18 = 5/9 = 0.5556`
`theta = cos^-1 0.5556 = 56.25`
∴ `2theta` = 112.5°
`cos2 theta = -0.38`
`"E" = sqrt((0.416 xx 10^6)^2 xx (0.69 xx 10^6)^2 + 2 xx 0.416 xx 0.69 xx 10^12 xx (-0.38))`
= `6.6 xx 10^5 "V m"^-1`
Therefore, the potential at a point 10 cm (perpendicular to the mid-point) is 2.0 × 105 V and electric field is 6.6 ×105 V m−1.
APPEARS IN
संबंधित प्रश्न
Deduce the expression for the potential energy of a system of two charges q1 and q2 located `vec(r_1)` and `vec(r_2)`, respectively, in an external electric field.
Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
Deduce the expression for the potential energy of a system of two point charges q1 and q2 brought from infinity to the points `vecr_1`and `vecr_2`respectively in the presence of external electric field `vecE`.
- In an external electric field, the positive and negative charges of a non–polar molecule are displaced in opposite directions.
- In non –polar molecules displacement stops when the external force on the constituent charges of the molecule is balanced by the restoring force.
- The non–polar molecule develops an induced dipole moment.
Two charges q1 and q2 are placed in a region with an external electric field E and corresponding potential V(r). What is the total potential energy of the system?
When bringing charge q1 from infinity to position r1 in an external electric field, what is the work done against the external field?
For two like charges (q1q2 > 0), the sign of the mutual Coulombic interaction energy \[\frac{q_1q_2}{4\pi\varepsilon_0 r_{12}}\] is __________, indicating a __________ force.
For two unlike charges (q1q2 < 0), what is the physical meaning of the negative mutual Coulombic interaction energy?
Given an external electric field with potential V(r) = A/r where A = 9 × 10⁵ N C⁻¹ m², what is the external potential at distance r = 0.09 m?
In the example with an external field E = A/r², the interaction energy of q1 = +7 μC with the external field at V(r1) = 10⁷ V is:
What is the primary analogy between gravitational potential energy and electric potential energy for a system of two masses/charges in an external field?
In what scenario is the potential energy of a two-charge system given by the formula \[U = \frac{q_1q_2}{4\pi\varepsilon_0 r_{12}}\] with no additional terms?
The three energy components in the potential energy formula for two charges in an external field represent:
For a two-charge system in an external field, if the external potential is positive and uniform, how do the energy contributions of a positive and negative charge differ?
