Advertisements
Advertisements
प्रश्न
Two tiny spheres carrying charges 1.5 μC and 2.5 μC are located 30 cm apart. Find the potential and electric field:
(a) at the mid-point of the line joining the two charges, and
(b) at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.
उत्तर
Two charges placed at points A and B are represented in the given figure. O is the mid-point of the line joining the two charges.

Magnitude of charge located at A, q1 = 1.5 μC
Magnitude of charge located at B, q2 = 2.5 μC
Distance between the two charges, d = 30 cm = 0.3 m
(a) Let V1 and E1 are the electric potentials and electric field respectively at O.
V1 = Potential due to charge at A + Potential due to charge at B
`"V"_1 = "q"_1/(4piin_0("d"/2)) + "q"_2/(4piin_0("d"/2)) = 1/(4piin_0("d"/2))("q"_1 + "q"_2)`
Where,
∈0 = Permittivity of free space
`1/(4piin_0) = 9 xx 10^9 "N C"^2 "m"^-2`
∴ `"V"_1 = (9 xx 10^9 xx 10^-6)/((0.30/2))(2.5 + 1.5)`
= `2.4 xx 10^5 "V"`
E1 = Electric field due to q2 − Electric field due to q1
= `"q"_2/(4piin_0("d"/2)^2) - "q"_1/(4piin_0("d"/2)^2)`
= `(9 xx 10^9)/((0.30/2)^2) xx 10^6 xx (2.5 - 1.5)`
= `4 xx 10^5 "V m"^-1`
Therefore, the potential at mid-point is 2.4 × 105 V and the electric field at mid-point is 4 × 105 V m−1. The field is directed from the larger charge to the smaller charge.
(b) Consider a point Z such that normal distance OZ = 10 cm = 0.1 m, as shown in the following figure.
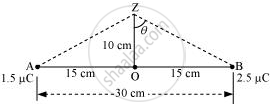
V2 and E2 are the electric potential and electric field respectively at Z.
It can be observed from the figure that distance,
`"BZ" = "AZ" = sqrt((0.1)^2 + (0.15)^2)` = 0.18 m
V2 = Electric potential due to A + Electric Potential due to B
= `"q"_1/(4piin_0("AZ")) + "q"_2/(4piin_0("BZ"))`
= `(9 xx 10^9 xx 10^-6)/0.18(1.5 + 2.5)`
Electric field due to q at Z,
`"E"_"A" = "q"_1/(4piin_0("AZ")^2)`
= `(9 xx 10^9 xx 1.5 xx 10^-6)/(0.18)^2`
= `0.416 xx 10^6 "V"/"m"`
Electric field due to q2 at Z,
`E_"B" = "q"_2/(4piin_0("BZ")^2)`
= `(9 xx 10^9 xx 2.5 xx 10^-6)/(0.18)^2`
= `0.69 xx 10^6 "V m"^-1`
The resultant field intensity at Z,
`"E" = sqrt("E"_"A"^2 + "E"_"B"^2 + 2"E"_"A""E"_"B"cos 2 theta)`
Where, 2θ is the angle, ∠AZB
From the figure, we obtain
`cos theta = 0.10/0.18 = 5/9 = 0.5556`
`theta = cos^-1 0.5556 = 56.25`
∴ `2theta` = 112.5°
`cos2 theta = -0.38`
`"E" = sqrt((0.416 xx 10^6)^2 xx (0.69 xx 10^6)^2 + 2 xx 0.416 xx 0.69 xx 10^12 xx (-0.38))`
= `6.6 xx 10^5 "V m"^-1`
Therefore, the potential at a point 10 cm (perpendicular to the mid-point) is 2.0 × 105 V and electric field is 6.6 ×105 V m−1.
APPEARS IN
संबंधित प्रश्न
Deduce the expression for the potential energy of a system of two charges q1 and q2 located `vec(r_1)` and `vec(r_2)`, respectively, in an external electric field.
Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
Two charges −q and +q are located at points (0, 0, −a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/a >> 1.
(c) How much work is done in moving a small test charge from the point (5, 0, 0) to (−7, 0, 0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
Deduce the expression for the potential energy of a system of two point charges q1 and q2 brought from infinity to the points `vecr_1`and `vecr_2`respectively in the presence of external electric field `vecE`.
- In an external electric field, the positive and negative charges of a non–polar molecule are displaced in opposite directions.
- In non –polar molecules displacement stops when the external force on the constituent charges of the molecule is balanced by the restoring force.
- The non–polar molecule develops an induced dipole moment.
