Advertisements
Advertisements
प्रश्न
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
काटकोन त्रिकोणात काटकोन करणाऱ्या बाजूंच्या वर्गांची बेरीज 169 असेल, तर त्याच्या कर्णाची लांबी किती?
विकल्प
15
13
5
12
उत्तर
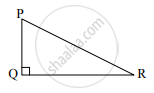
ΔPQR मध्ये, ∠Q = 90°
∴ PR2 = PQ2 + QR2 .....…[पायथागोरसचे प्रमेय]
∴ PR2 = 169
∴ PR = `sqrt(169)` = 13
काटकोन त्रिकोणात काटकोन करणाऱ्या बाजूंच्या वर्गांची बेरीज 169 असेल, तर त्याच्या कर्णाची लांबी 13 असेल.
संबंधित प्रश्न
आकृती मध्ये ∠DFE = 90°, रेख FG ⊥ रेख ED. जर GD = 8, FG = 12, तर (1) EG (2) FD आणि (3) EF काढा.
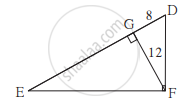
आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर आयताच्या कर्णाची लांबी काढा.
प्रणाली आणि प्रसाद एकाच ठिकाणावरून पूर्व आणि उत्तर दिशेला सारख्या वेगाने निघाले. दोन तासांनंतर त्यांच्यामधील अंतर `15sqrt2` किमी असेल तर त्यांचा ताशी वेग काढा.
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका आयताची एक बाजू 12 आणि कर्णाची लांबी 20 असेल, तर त्या आयताच्या दुसऱ्या बाजूची लांबी किती?
एका काटकोन त्रिकोणामध्ये कर्णाची लांबी 25 सेमी व उंची 7 सेमी असेल, तर त्याच्या पायाची लांबी काढा.
सोबतच्या आकृतीत, ∆ABC मध्ये, AD ⊥ BC, तर AB2 + CD2 = BD2 + AC2 हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
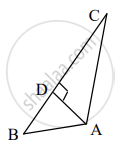
कृती: पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ADC मध्ये,
AC2 = AD2 + `square^2`
∴ AD2 = AC2 – CD2 …...........(i)
तसेच, पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ABD मध्ये,
AB2 = `square^2` + BD2
∴ AD2 = AB2 – BD2 …...… (ii)
∴ `square^2 - "BD"^2 = "AC"^2 - square^2` .....…….. (i) व (ii) वरून
∴ AB2 + CD2 = AC2 + BD2
सोबतच्या आकृतीत, ∠DFE = 90°, FG ⊥ ED, जर GD = 8, FG = 12, lej (1) EG, (2) FD आणि (3) EF काढा.
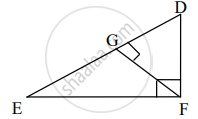
समद्विभुज काटकोन त्रिकोणाच्या एकरूप बाजूंची लांबी 7 सेमी आहे. त्याची परिमिती काढा.
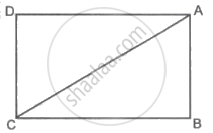
वरील आकृतीत `square`ABCD हा आयत आहे. जर AB = 5, AC = 13, तर बाजू BC ची लांबी काढण्यासाठी खालील कृती पर्ण करा.
कृती: ΔABC हा `square` त्रिकोण आहे.
∴ पायथागोरसच्या प्रमेयानुसार,
AB2 + BC2 = AC2
∴ 25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
3 सेमी व 5 सेमी त्रिज्या आणि केंद्र O असलेली दोन एककेंद्री वर्तुळे काढा. मोठया वर्तुळावर कोणताही एक A बिंदू घ्या. बिंदू A मधून लहान वर्तुळाला स्पर्शिका काढा. त्या स्पर्शिकाखंडाची लांबी मोजा व लिहा. पायथागोरसच्या प्रमेयाचा उपयोग करून स्पर्शिकाखंडाची लांबी काढा.
