Advertisements
Advertisements
प्रश्न
उस रैखिक समीकरण का आलेख खींचिए जिसके हल उन बिंदुओं से निरूपित हैं, जिनके निर्देशांकों का योग 10 इकाई है।
उत्तर
प्रश्न के अनुसार, निर्देशांकों का योग 10 इकाई है।
मान लीजिए कि x और y दो निर्देशांक हैं, तो हमें x + y = 10 प्राप्त होता है।
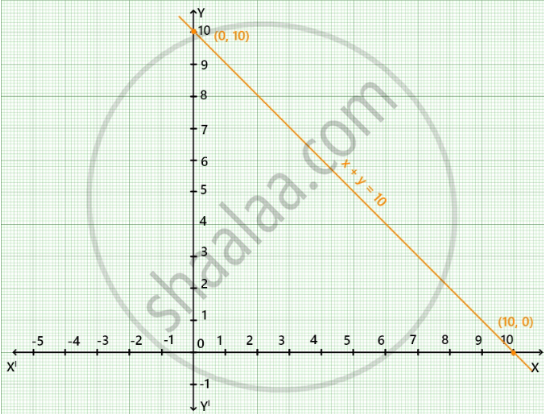
x = 5 के लिए, y = 5, इसलिए, (5, 5) x + y = 10 के आलेख पर स्थित है।
x = 3 के लिए, y = 7, इसलिए, (3, 7) x + y = 10 के आलेख पर स्थित है।
अब, बिंदुओं (5, 5) और (3, 7) को ग्राफ पेपर पर आलेखित करके उन्हें एक रेखा से जोड़ने पर हमें रैखिक समीकरण x + y = 10 का ग्राफ प्राप्त होता है।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित रैखिक समीकरणों का दो चरों में आलेख खींचिए:- x - y = 2
निम्नलिखित रैखिक समीकरणों का दो चरों में आलेख खींचिए:- 3 = 2x + y
यदि बिंदु (3, 4) समीकरण 3y = ax + 7 के आलेख पर स्थित है, तो a का मान ज्ञात कीजिए |
एक नगर में टैक्सी का किराया निम्नलिखित है: पहले किलोमीटर का किराया 8 रु है और उसके बाद की दूरी के लिए प्रति किलोमीटर का किराया 5 रु है। यदि तय की गई दूरी x किलोमीटर हो, और कुल किराया y रु हो, तो इसका एक रैखिक समीकरण लिखिए और उसका आलेख खींचिए।
नीचे दिए गए विकल्पों में से उस समीकरण को चुनिए जिसके आलेख दिए गए आंकड़ों में दिए गए हैं।
पहले आंकड़े के लिए
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x

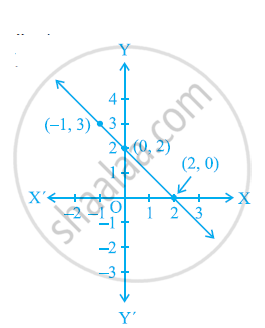
दूसरे आंकड़े के लिए
(i) y = x +2
(ii) y = x − 2
(iii) y = − x + 2
(iv) x + 2y = 6
एक अचर बल लगाने पर एक पिंड द्वारा किया गया कार्य पिंड द्वारा तय की गई दूरी के अनुक्रमानुपाती होता है। इस कथन को दो चरों वाले एक समीकरण के रूप में व्यक्त कीजिए और अचर बल 5 मात्रक लेकर इसका आलेख खींचिए। यदि पिंड द्वारा तय की गई दूरी
(i) 2 मात्रक (ii) 0 मात्रक
हो, तो आलेख से किया हुआ कार्य ज्ञात कीजिए।
x = 5, y = 2 निम्नलिखित रैखिक समीकरण का एक हल है
समीकरण ax + by + c = 0 के धनात्मक हल सदैव निम्नलिखित में स्थित होते हैं
(a, – a) रूप का बिंदु सदैव रेखा पर स्थित होता है
दो चरों वाली रैखिक समीकरण के आलेख का एक सरल रेखा होना आवश्यक नहीं है।
