Advertisements
Advertisements
प्रश्न
Use Huygens’ geometrical construction to show the propagation of plane wavefront a rarer medium (1) to a denser medium (2) undergoing refraction.
Hence derive Snell’s law of refraction.
उत्तर
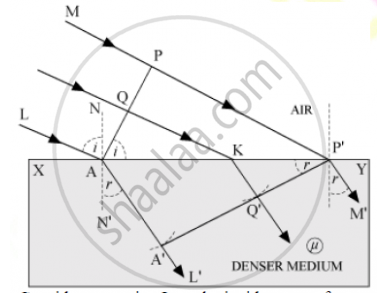
Consider any point Q on the incident wavefront.
Suppose when disturbance from point P on incident wavefront reaches point P’ on the refracted wavefront, the disturbance from point Q reaches Q’on the refracting surface XY. Since represents the refracted wavefront, the time taken by light to travel from a point on incident wavefront to the corresponding point on refracted wavefront should always be the same. Now, time taken by light to go from Q to Q’ will be
`t =(QK)/c +(KQ')/v ......... (1)`
In right-angled ΔAQK, ∠QAK = i
∴ QK = AK sin i … (ii)
In right-angled Δ P′Q′K,<q′p′k p=""></q′p′k>
KQ′ = KP′ sin r ………….(iii)
Substituting (ii) and (iii) in equation (i),
`t= (AK sin i)/c +(KP'sinr)/v`
`t =(AK sini)/c +((AP' -AK)sinr)/v`
`or, t =(Ap')/v sinr +(sini/c - sinr/v) AK ...... (4)`
The rays from different points on the incident wavefront will take the same time to reach the corresponding points on the refracted wavefront i.e., given by equation (iv) is independent of AK. It will happen so, if
`sini/c -sinr/v =0`
`sini/sinr = c/v`
However, `c/v = n`
`sini/sinr = n`
This is the Snell’s law for refraction of light.
संबंधित प्रश्न
Calculate the speed of light in a medium whose critical angle is 45°. Does critical angle for a given pair of media depend on the wavelength of incident light ? Give reason.
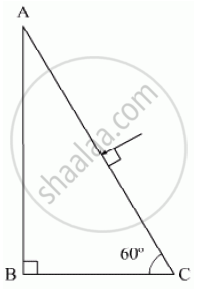
Trace the path of a ray of light passing through a glass prism (ABC) as shown in the figure. If the refractive index of glass is `sqrt3`, find out the value of the angle of emergence from the prism.
Find a critical angle for glass and water pair, given the refractive index of glass, is 1 ·62 and that of water is 1 ·33.
Derive Snell’s law of refraction using Huygens’s wave theory.
Define the term, “refractive index” of a medium. Verify Snell’s law of refraction when a plane wavefront is propagating from a denser to a rarer medium. Solution
Answer the following question.
Define the term, "refractive index" of a medium. Verify Snell's law of refraction when a plane wavefront is propagating from a denser to a rarer medium.
Draw the shape of refracted wavefront when the plane incident wave undergoes refraction from optically denser medium to rarer medium. Hence prove Snell’s law of refraction.
The mixture a pure liquid and a solution in a long vertical column (i.e, horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d << h, the height of the column.
If light passes near a massive object, the gravitational interaction causes a bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by n(r) = 1 + 2 GM/rc2 where r is the distance of the point of consideration from the centre of the mass of the massive body, G is the universal gravitational constant, M the mass of the body and c the speed of light in vacuum. Considering a spherical object find the deviation of the ray from the original path as it grazes the object.
A ray of light is incident on a glass prism of refractive index µ and refracting angle A. If it just suffers total internal reflection at the other face, obtain a relation between the angle of incidence, angle of prism and critical angle.
