Advertisements
Advertisements
प्रश्न
Using Bohr's postulates, derive the expression for the orbital period of the electron moving in the nth orbit of hydrogen atom ?
उत्तर
According to Bohr's model, the centripetal force required for the revolution of electrons around the nucleus is provided by the electrostatic force of attraction between the electron and the nucleus.
If m is the mass of electron moving with a velocity v in a circular orbit of radius r, then the necessary centripetal force is \[F = \frac{m v^2}{r} . . . . . (i)\]
Also, the electrostatic force of attraction between the nucleus of charge (+Ze) and electron of charge (-e) is
\[F = \frac{1}{4\pi \epsilon_o}\frac{Z e^2}{r^2} = \frac{KZ e^2}{r^2} . . . . . (ii)\]
\[\text { where }, K = \frac{1}{4\pi \epsilon_o}\]
From (i) and (ii)
\[\frac{m v^2}{r} = \frac{KZ e^2}{r^2} \]
\[ \Rightarrow r = \frac{KZ e^2}{m v^2} . . . . . (iii)\]
Also one of the Bohr’s postulates states that the electron revolves in stationary orbits where the angular momentum of electron is an integral multiple of h/2π.
\[mvr = \frac{nh}{2\pi}\]
Here, h is Planck's constant and n is any positive integer, 1, 2, 3...
\[\Rightarrow r = \frac{nh}{2\pi vm} . . . . . (iv)\]
From (iii) and (iv), we get
\[\frac{KZ e^2}{m v^2} = \frac{nh}{2\pi mv}\]
\[or\]
\[v = \frac{2\pi KZ e^2}{nh} . . . . . (v)\]
Now, we know frequency (\[\nu\]) of electron in Bohr's stationary orbit is given by
\[v = r\omega = r(2\pi\nu)\]
\[\nu = \frac{v}{2\pi r}\]
\[\text { From (v), we get }\]
\[\nu = \frac{v}{2\pi r} = \frac{2\pi KZ e^2}{nh . 2\pi r} = \frac{KZ e^2}{nhr}\]
\[\nu = \frac{{KZe}^2}{nhr} \]
Now, we know the orbital period (T) of the electron moving in the nth orbit of hydrogen atom is related to (\[\nu\]) as \[T = \frac{1}{\nu}\]
\[ \Rightarrow T = \frac{nhr}{{Ke}^2}\]
APPEARS IN
संबंधित प्रश्न
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
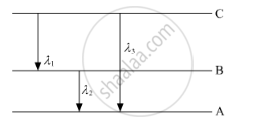
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
Draw a neat, labelled energy level diagram for H atom showing the transitions. Explain the series of spectral lines for H atom, whose fixed inner orbit numbers are 3 and 4 respectively.
The radius of the innermost electron orbit of a hydrogen atom is 5.3 × 10−11 m. What are the radii of the n = 2 and n = 3 orbits?
State Bohr postulate of hydrogen atom that gives the relationship for the frequency of emitted photon in a transition.
When a photon stimulates the emission of another photon, the two photons have
(a) same energy
(b) same direction
(c) same phase
(d) same wavelength
What is the energy in joules released when an electron moves from n = 2 to n = 1 level in a hydrogen atom?
The energy associated with the first orbit of He+ is ____________ J.
According to Bohr’s theory, the angular momentum of an electron in 5th orbit is ______.
An electron in H-atom makes a transition from n = 3 to n = 1. The recoil momentum of the H-atom will be ______.
According to Bohr's theory, the radius of the nth Bohr orbit of a hydrogen like atom of atomic number Z is proportional to ______.
