Advertisements
Advertisements
प्रश्न
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
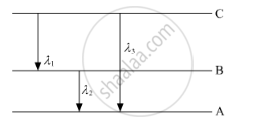
उत्तर
(a) Bohr's quantisation condition: According to Bohr, an electron can revolve only in certain discrete, non-radiating orbits for which total angular momentum of the revolving electron is an integral multiple of `h/(2pi)`where h is the Planck's constant.
`:.mvr=(nh)/(2pi)`
(b) Using the Rydberg formula of the spectra of hydrogen atom, we write
`1/lamda_1=R(1/n_(2^2)-1/n_(3^2)) ......(1)`
`1/lamda_2=R(1/n_(1^2)-1/n_(2^2)) ......(2)`
`1/lamda_3=R(1/n_(1^2)-1/n_(3^2)) ......(3)`
Adding (1) and (2), we find that
`1/lambda_1+1/(lambda_2)=R(1/n_(1^2)-1/n_(3^2))=1/lambda_3`
This is the required relation between the three wavelengths.
संबंधित प्रश्न
State Bohr’s postulate of hydrogen atom which successfully explains the emission lines in the spectrum of hydrogen atom. Use Rydberg formula to determine the wavelength of Hα line. [Given: Rydberg constant R = 1.03 × 107 m−1]
In accordance with the Bohr’s model, find the quantum number that characterises the earth’s revolution around the sun in an orbit of radius 1.5 × 1011 m with orbital speed 3 × 104 m/s. (Mass of earth = 6.0 × 1024 kg)
Radiation from hydrogen discharge tube falls on a cesium plate. Find the maximum possible kinetic energy of the photoelectrons. Work function of cesium is 1.9 eV.
Consider a neutron and an electron bound to each other due to gravitational force. Assuming Bohr's quantization rule for angular momentum to be valid in this case, derive an expression for the energy of the neutron-electron system.
A particle has a mass of 0.002 kg and uncertainty in its velocity is 9.2 × 10−6 m/s, then uncertainty in position is ≥ ____________.
(h = 6.6 × 10−34 J s)
The energy associated with the first orbit of He+ is ____________ J.
Find the ratio of energies of photons produced due to transition of an election of hydrogen atom from its (i) second permitted energy level to the first level. and (ii) the highest permitted energy level to the first permitted level.
The energy required to remove the electron from a singly ionized Helium atom is 2.2 times the energy required to remove an electron from Helium atom. The total energy required to ionize the Helium atom completely is ______.
Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-Broglie wavelengths of the particle. For a charged particle moving in a plane perpendicular to a magnetic field, the radius of the nth orbital will therefore be proportional to:
In hydrogen atom, transition from the state n = 6 to n = 1 results in ultraviolet radiation. Infrared radiation will be obtained in the transition ______.
