Advertisements
Advertisements
प्रश्न
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
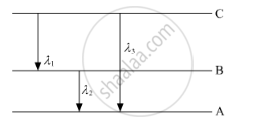
उत्तर
(a) Bohr's quantisation condition: According to Bohr, an electron can revolve only in certain discrete, non-radiating orbits for which total angular momentum of the revolving electron is an integral multiple of `h/(2pi)`where h is the Planck's constant.
`:.mvr=(nh)/(2pi)`
(b) Using the Rydberg formula of the spectra of hydrogen atom, we write
`1/lamda_1=R(1/n_(2^2)-1/n_(3^2)) ......(1)`
`1/lamda_2=R(1/n_(1^2)-1/n_(2^2)) ......(2)`
`1/lamda_3=R(1/n_(1^2)-1/n_(3^2)) ......(3)`
Adding (1) and (2), we find that
`1/lambda_1+1/(lambda_2)=R(1/n_(1^2)-1/n_(3^2))=1/lambda_3`
This is the required relation between the three wavelengths.
संबंधित प्रश्न
Find the frequency of revolution of an electron in Bohr’s 2nd orbit; if the radius and speed of electron in that orbit is 2.14 × 10-10 m and 1.09 × 106 m/s respectively. [π= 3.142]
If the velocity of the electron in Bohr’s first orbit is 2.19 × 106 ms-1, calculate the de Broglie wavelength associated with it.
The ratio of kinetic energy of an electron in Bohr’s orbit to its total energy in the same orbit is
(A) – 1
(B) 2
(C) 1/2
(D) – 0.5
Using Bohr’s postulates for hydrogen atom, show that the total energy (E) of the electron in the stationary states tan be expressed as the sum of kinetic energy (K) and potential energy (U), where K = −2U. Hence deduce the expression for the total energy in the nth energy level of hydrogen atom.
Write the expression for Bohr’s radius in hydrogen atom ?
The binding energy of a H-atom, considering an electron moving around a fixed nuclei (proton), is B = `- (Me^4)/(8n^2ε_0^2h^2)`. (m = electron mass). If one decides to work in a frame of reference where the electron is at rest, the proton would be moving around it. By similar arguments, the binding energy would be
B = `- (Me^4)/(8n^2ε_0^2h^2)` (M = proton mass)
This last expression is not correct because ______.
The ground state energy of hydrogen atoms is -13.6 eV. The photon emitted during the transition of electron from n = 3 to n = 1 unknown work function. The photoelectrons are emitted from the material with a maximum kinetic energy of 9 eV. Calculate the threshold wavelength of the material used.
A 100 eV electron collides with a stationary helium ion (He+) in its ground state and exits to a higher level. After the collision, He+ ions emit two photons in succession with wavelengths 1085 Å and 304 Å. The energy of the electron after the collision will be ______ eV.
Given h = 6.63 × 10-34 Js.
What is the energy of an electron in stationary state corresponding to n = 2?
Oxygen is 16 times heavier than hydrogen. Equal volumes of hydrogen and oxygen are mixed. The ratio of speed of sound in the mixture to that in hydrogen is ______.
