Advertisements
Advertisements
प्रश्न
The ratio of kinetic energy of an electron in Bohr’s orbit to its total energy in the same orbit is
(A) – 1
(B) 2
(C) 1/2
(D) – 0.5
उत्तर
(A) – 1
APPEARS IN
संबंधित प्रश्न
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
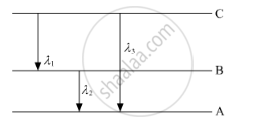
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
Draw a neat, labelled energy level diagram for H atom showing the transitions. Explain the series of spectral lines for H atom, whose fixed inner orbit numbers are 3 and 4 respectively.
The longest wavelength doublet absorption transition is observed at 589 and 589.6 nm. Calculate the frequency of each transition and energy difference between two excited states.
If the photon of the wavelength 150 pm strikes an atom and one of its inner bound electrons is ejected out with a velocity of 1.5 × 107 ms–1, calculate the energy with which it is bound to the nucleus.
The gravitational attraction between electron and proton in a hydrogen atom is weaker than the Coulomb attraction by a factor of about 10−40. An alternative way of looking at this fact is to estimate the radius of the first Bohr orbit of a hydrogen atom if the electron and proton were bound by gravitational attraction. You will find the answer interesting.
Using Bohr’s postulates, obtain the expressions for (i) kinetic energy and (ii) potential energy of the electron in stationary state of hydrogen atom.
Draw the energy level diagram showing how the transitions between energy levels result in the appearance of Lymann Series.
Using Bohr’s postulates for hydrogen atom, show that the total energy (E) of the electron in the stationary states tan be expressed as the sum of kinetic energy (K) and potential energy (U), where K = −2U. Hence deduce the expression for the total energy in the nth energy level of hydrogen atom.
The difference in the frequencies of series limit of Lyman series and Balmer series is equal to the frequency of the first line of the Lyman series. Explain.
The numerical value of ionization energy in eV equals the ionization potential in volts. Does the equality hold if these quantities are measured in some other units?
Calculate the magnetic dipole moment corresponding to the motion of the electron in the ground state of a hydrogen atom.
A neutron moving with a speed υ strikes a hydrogen atom in ground state moving towards it with the same speed. Find the minimum speed of the neutron for which inelastic (completely or partially) collision may take place. The mass of neutron = mass of hydrogen = 1.67 × 10−27 kg.v
Light from Balmer series of hydrogen is able to eject photoelectrons from a metal. What can be the maximum work function of the metal?
If l3 and l2 represent angular momenta of an orbiting electron in III and II Bohr orbits respectively, then l3: l2 is :
Answer the following question.
Calculate the de-Broglie wavelength associated with the electron revolving in the first excited state of the hydrogen atom. The ground state energy of the hydrogen atom is – 13.6 eV.
The radius of the third Bohr orbit for hydrogen atom is ____________.
For an electron in the second orbit of hydrogen, what is the moment of momentum as per the Bohr's model?
According to the Bohr theory of H-atom, the speed of the electron, its energy and the radius of its orbit varies with the principal quantum number n, respectively, as:
The energy of an electron in hth orbit of hydrogen atom is –13.6/n2ev energy required to excite the electron from the first orbit to the third orbit is
The ratio of the ionization energy of H and Be+3 is ______.
The Bohr model for the spectra of a H-atom ______.
- will not be applicable to hydrogen in the molecular from.
- will not be applicable as it is for a He-atom.
- is valid only at room temperature.
- predicts continuous as well as discrete spectral lines.
The inverse square law in electrostatics is |F| = `e^2/((4πε_0).r^2)` for the force between an electron and a proton. The `(1/r)` dependence of |F| can be understood in quantum theory as being due to the fact that the ‘particle’ of light (photon) is massless. If photons had a mass mp, force would be modified to |F| = `e^2/((4πε_0)r^2) [1/r^2 + λ/r]`, exp (– λr) where λ = mpc/h and h = `h/(2π)`. Estimate the change in the ground state energy of a H-atom if mp were 10-6 times the mass of an electron.
The energy required to remove the electron from a singly ionized Helium atom is 2.2 times the energy required to remove an electron from Helium atom. The total energy required to ionize the Helium atom completely is ______.
The first ionization energy of H is 21.79 × 10-19 J. The second ionization energy of He atom is ______ × 10-19J.
A hydrogen atom in is ground state absorbs 10.2 eV of energy. The angular momentum of electron of the hydrogen atom will increase by the value of ______.
(Given, Planck's constant = 6.6 × 10-34 Js)
An electron in a hydrogen atom has an energy of -3.4 eV. The difference between its kinetic and potential energy is ______.
State the Bohr's postulate of angular momentum of an electron.
What is the velocity of an electron in the 3rd orbit of hydrogen atom if its velocity in the 1st orbit is v0?
The de Broglie wavelength of an electron in the first Bohr’s orbit of hydrogen atom is equal to ______.
