Question

Using Bohr’s postulates, obtain the expressions for (i) kinetic energy and (ii) potential energy of the electron in stationary state of hydrogen atom.

Draw the energy level diagram showing how the transitions between energy levels result in the appearance of Lymann Series.

Answer 1

According to Bohr’s postulates, in a hydrogen atom, a single alectron revolves around a nucleus of charge +e. For an electron moving with a uniform speed in a circular orbit os a given radius, the centripetal force is provided by Columb force of attraction between the electron and the nucleus. The gravitational attraction may be neglected as the mass of electron and proton is very small.

So,

`mv^2/r = (ke^2)/r^2`

0r `mv^2 = (ke^2)/r   ...................(1)`

where m = mass of electron

r = radius of electronic orbit

v = velocity of electron.

Again,

`mvr = (nh)/(2π)`

` or v = (nh)/(2πmr)`

From eq(1), we get,

`m ((nh)/(2πmr))^2 = (ke^2)/r`

`⇒ r = (n^2h^2)/(4π^2kme^2)      .....................(2) `

(i) Kinetic energy of electron,

`E_k = 1/2mv^2 = (ke^2)/(2r)`

Using eq (2), we get

`E_k = (ke^2)/2 (4π^2kme^2)/(n^2h^2)`

= `(2π^2k^2me^4)/(n^2h^2)`

(ii) Potential energy

`E^p= - ke^2 xx (4π^2k^2me^4)/(n^2h^2) `

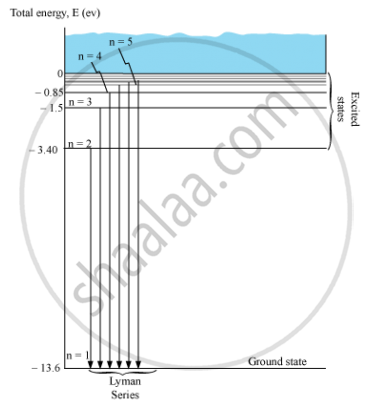
Energy level diagram showing the transitions between energy levels result in the appearance ofLymann series:

For Lymann series, n_f = 1 and n_i = 2, 3, 4, 5, …

`1/λ = R_H(1/I^2 - 1/n^2)`

Where, n_i = 2, 3, 4, 5, …