Advertisements
Advertisements
Question
Using Bohr’s postulates, obtain the expressions for (i) kinetic energy and (ii) potential energy of the electron in stationary state of hydrogen atom.
Draw the energy level diagram showing how the transitions between energy levels result in the appearance of Lymann Series.
Advertisements
Solution
According to Bohr’s postulates, in a hydrogen atom, a single alectron revolves around a nucleus of charge +e. For an electron moving with a uniform speed in a circular orbit os a given radius, the centripetal force is provided by Columb force of attraction between the electron and the nucleus. The gravitational attraction may be neglected as the mass of electron and proton is very small.
So,
`mv^2/r = (ke^2)/r^2`
0r `mv^2 = (ke^2)/r ...................(1)`
where m = mass of electron
r = radius of electronic orbit
v = velocity of electron.
Again,
`mvr = (nh)/(2π)`
` or v = (nh)/(2πmr)`
From eq(1), we get,
`m ((nh)/(2πmr))^2 = (ke^2)/r`
`⇒ r = (n^2h^2)/(4π^2kme^2) .....................(2) `
(i) Kinetic energy of electron,
`E_k = 1/2mv^2 = (ke^2)/(2r)`
Using eq (2), we get
`E_k = (ke^2)/2 (4π^2kme^2)/(n^2h^2)`
= `(2π^2k^2me^4)/(n^2h^2)`
(ii) Potential energy
`E^p= - ke^2 xx (4π^2k^2me^4)/(n^2h^2) `
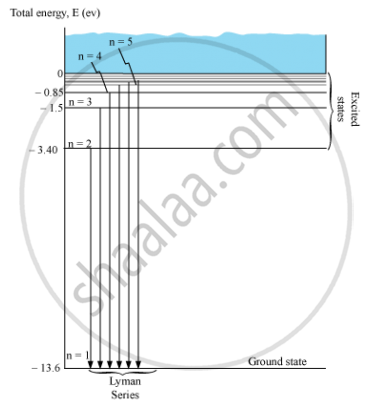
Energy level diagram showing the transitions between energy levels result in the appearance ofLymann series:
For Lymann series, nf = 1 and ni = 2, 3, 4, 5, …
`1/λ = R_H(1/I^2 - 1/n^2)`
Where, ni = 2, 3, 4, 5, …
APPEARS IN
RELATED QUESTIONS
Evaluate Rydberg constant by putting the values of the fundamental constants in its expression.
A beam of monochromatic light of wavelength λ ejects photoelectrons from a cesium surface (Φ = 1.9 eV). These photoelectrons are made to collide with hydrogen atoms in ground state. Find the maximum value of λ for which (a) hydrogen atoms may be ionized, (b) hydrogen atoms may get excited from the ground state to the first excited state and (c) the excited hydrogen atoms may emit visible light.
A filter transmits only the radiation of wavelength greater than 440 nm. Radiation from a hydrogen-discharge tube goes through such a filter and is incident on a metal of work function 2.0 eV. Find the stopping potential which can stop the photoelectrons.
Mention demerits of Bohr’s Atomic model.
If the radius of first electron orbit in hydrogen atom be r then the radius of the fourth orbit ill be ______.
The energy of an electron in hth orbit of hydrogen atom is –13.6/n2ev energy required to excite the electron from the first orbit to the third orbit is
Taking the Bohr radius as a0 = 53 pm, the radius of Li++ ion in its ground state, on the basis of Bohr’s model, will be about ______.
The inverse square law in electrostatics is |F| = `e^2/((4πε_0).r^2)` for the force between an electron and a proton. The `(1/r)` dependence of |F| can be understood in quantum theory as being due to the fact that the ‘particle’ of light (photon) is massless. If photons had a mass mp, force would be modified to |F| = `e^2/((4πε_0)r^2) [1/r^2 + λ/r]`, exp (– λr) where λ = mpc/h and h = `h/(2π)`. Estimate the change in the ground state energy of a H-atom if mp were 10-6 times the mass of an electron.
A 20% efficient bulb emits light of wavelength 4000 Å. If the power of the bulb is 1 W, the number of photons emitted per second is ______.
[Take, h = 6.6 × 10-34 J-s]
The energy of an electron in the nth orbit of the hydrogen atom is En = -13.6/n2eV. The negative sign of energy indicates that ______.
