Question

Using vectors prove that the altitudes of a triangle are concurrent.

Answer 1

Let, the altitudes AD and BE intersect at O

Join CO and produce to meet AB in F

Let `vec(OA) = veca`

`vec(OB) = vecb. vec(OC) = vecc`

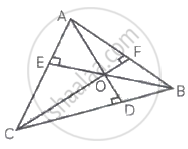
`veca` is perpendicular to `vec(BC) = vec(OC) = vecc - vecb`

Therefore, `veca. (vecc - vecb)` = 0

⇒ `veca.vecb = veca.vecb`  ......(i)

Also direction OB is perpendicular to AC.

∴ `vecb.(vecc - veca)` = 0

⇒ `vecb. vecc = veca . vecb`  ......(ii)

From equations (i) and (ii), we get

`veca.vecc = veca.vecb = vecb.vecc`

i.e., `vecc.veca - vecc.vecb` = 0

⇒ `vecc. (veca - vecb)` = 0  ......(iii)

`veca - vecb = vec(OA) - vec(OB) = vec(BA)` 

And by virtue of equation (iii), `vecC` is perpendicular to ``vec(BA), but `vecC` is a vector in direction of `vec(OC)`

Hence, `vec(OC)` is perpendicular to `vec(AB)`, i.e., CF is the third altitude of the triangle through C.

Hence. the 3 altitudes are concurrent at O.