Advertisements
Advertisements
Question
Using vectors prove that the altitudes of a triangle are concurrent.
Solution
Let, the altitudes AD and BE intersect at O
Join CO and produce to meet AB in F
Let `vec(OA) = veca`
`vec(OB) = vecb. vec(OC) = vecc`
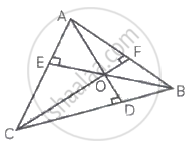
`veca` is perpendicular to `vec(BC) = vec(OC) = vecc - vecb`
Therefore, `veca. (vecc - vecb)` = 0
⇒ `veca.vecb = veca.vecb` ......(i)
Also direction OB is perpendicular to AC.
∴ `vecb.(vecc - veca)` = 0
⇒ `vecb. vecc = veca . vecb` ......(ii)
From equations (i) and (ii), we get
`veca.vecc = veca.vecb = vecb.vecc`
i.e., `vecc.veca - vecc.vecb` = 0
⇒ `vecc. (veca - vecb)` = 0 ......(iii)
`veca - vecb = vec(OA) - vec(OB) = vec(BA)`
And by virtue of equation (iii), `vecC` is perpendicular to ``vec(BA), but `vecC` is a vector in direction of `vec(OC)`
Hence, `vec(OC)` is perpendicular to `vec(AB)`, i.e., CF is the third altitude of the triangle through C.
Hence. the 3 altitudes are concurrent at O.
APPEARS IN
RELATED QUESTIONS
If a line makes angle 90°, 60° and 30° with the positive direction of X, Y and Z axes respectively, find its direction cosines
If `bar"u" = hat"i" - 2hat"j" + hat"k", bar"r" = 3hat"i" + hat"k"` and `bar"w" = hat"j", hat"k"` are given vectors , then find `[bar"u" + bar"w"]*[(bar"w" xx bar"r") xx (bar"r" xx bar"w")]`
If `veca + vecb, vecb + vecc` and `vecc + veca` are coterminous edges of a parallelepiped then its volume is ______.
The angle between the planes and `bar"r"*(2hat"i" + hat"j" - hat"k") = 3` and `bar"r"*(hat"i" + 2hat"j" + hat"k") = 1` is ______.
Let `bar"a" = 2hat"i" + hat"j" - 2hat"k" and bar"b" = hat"i" + hat"j"`. If `bar"c"` is a vector such that `bar"a" bar"c" = |bar"c"|, |bar"c" - bar"a"| = 2sqrt2` and the angle between `bar"a" xx bar"b" and bar"c"` is 30°, then `|bar"a" xx (bar"b" xx bar"c")|` = ______.
The angle between the line `bar"r" = (hat"i" + 2hat"j" + hat"k") + lambda(hat"i" + hat"j" + hat"k")` and the plane `bar"r"*(2hat"i" - hat"j" + hat"k")` = 8 is ______.
The value of `hati . (hatj xx hatk) + hatj . (hatk xx hati) + hatk . (hati xx hatj)` is ______
The direction ratios 3x – 2 = 2y + 1 = 3z – 3 are ______.
Let `bar"a"` and `bar"b"` be two unit vectors. If the vectors `bar"c" = bar"a" + 2bar"b"` and `bar"d" = 5bar"a" - 4bar"b"` are perpendicular to each other, then the angle between `bar"a"` and `bar"b"` is ______.
The equation of line passing through (3, –1, 2 ) and perpendicular to the lines
`vecr = (hati + hatj - hatk) + λ(2hati - 2hatj + hatk)` and
`vecr = (2hati + hatj - 3hatk) + μ(hati - 2hatj + 2hatk)` is:
If vector r with dc's l, m, n is equally inclined to the coordinate axes, then the total number of such vectors is ______.
Direction cosines of the line `(x + 2)/2 = (2y - 5)/3, z = -1` are ______.
Direction ratios of the line which is perpendicular to the lines with direction ratios –1, 2, 2 and 0, 2, 1 are ______.
What will be projection of the vector `4hati - 3hatj + hatk` on the line joining the points (2, 3, – 1) and (– 2, – 4, 3)?
Determine whether `bara " and" barb` are orthogonal, parallel or neither.
`bara=-3/5hati +1/2hatj +1/3hatk, barb= 5hati+4hatj+3hatk `
If a vector has direction angles 45º and 60º find the third direction angle.
If `|bara| = |barb|` = 1 and `|bara + barb| = sqrt(3)`, then the value of `(3bara - 4barb)*(2bara + 5barb)` = ______.
Find the projection of `bar(AB)` on `bar(CD)`, where A ≡ (2, –3, 0), B ≡ (1, –4, –2), C ≡ (4, 6, 8), D ≡ (7, 0, 10).
If `|bara + barb| = |bara - barb|, bara` and `barb` are non-zero vectors, find the angle between `bara` and `barb`.
If `bara` and `barb` are unit vectors, then the angle between `bara` and `barb` for `(sqrt(3)bara - barb)` be a unit vector, is ______.
If θ is the acute angle between the vectors `hati + hatj + hatk` and `2hati - hatj + hatk`, then tan θ is ______.
If a vector has direction angles 45° and 60° find the third direction angle.
Find the angle between the line `bar r = (hat i + 2hat j + hat k) + lambda(hat i + hat j + hat k)` and the plane `bar r *(2hat i + hat j + hat k) = 8`.
Determine whether `bb(bara)` and `bb(barb)` are orthogonal, parallel, or neither.
`bara = -3/5 hati + 1/2 hatj +1/3 hatk, barb = 5 hati + 4 hatj + 3 hatk`
If a vector has direction angles 45° and 60° find the third direction angle.
If a vector has direction angles 45º and 60º, find the third direction angle.
If a vector has direction angles 45º and 60º find the third direction angle.
Determine whether `bara and barb` are orthogonal, parallel or neither.
`bara = -3/5hati + 1/2 hatj + 1/3hatk, barb = 5 hati + 4hatj + 3hatk`
If a vector has direction angles 45ºand 60º find the third direction angle.
If a vector has direction angles 45° and 60° find the third direction angle.
Find two unit vectors each of which is perpendicular to both `baru` and `barv`, where `baru = 2hati + hatj - 2hatk, barv = hati + 2hatj - 2hatk`.
Determine whether `bara and barb` and are orthogonal, parallel or neither.
`bara = -3/5hati + 1/2hatj + 1/3hatk, barb = 5hati + 4hatj + 3hatk`
